2.1.8.1 The Iterator Pattern

Before we present a complete implementation of singly-linked mutable lists, we describe a new pattern which allows us to process lists similarly to arrays. The pattern is called the Iterator pattern, and consists of two interfaces, an abstract list, with methods for building and modifying lists

interface ListI {
  /** inserts item at front of list */
  void insertFront(T item);     

  /** inserts item at rear of list */  
  void insertRear(T item);      

  /** returns true iff the list is empty */
  boolean isEmpty();              

  /** removes item at front of list */
  void removeFront();          

  /** returns an iterator for the list with cursor at front */
  IteratorI newIterator();
}

and an abstract iterator, with methods for traversing a list and examining its contents

interface IteratorI {
  /** moves the cursor to the front of the list */
  void front();        
  /** moves the cursor to the next item of the list */
  void next();                    
  /** returns true iff the cursor is at the end of the list */
  boolean atEnd();     
  /** returns the current item in the list */
  T currentItem();     
}

The iterator's atEnd method returns true if and only if the iterator has moved past the last element of the list. When atEnd() is true, the currentItem method will throw an exception.

With such a list and such an iterator we could easily implement a queue, since we can remove from the front and add at the back.

It would be nice if the list were more flexible however. For example, we may wish to sort a list. We can already do this in a functional style, by building a new list while using insertion sort, but since this is a mutable list we should ideally be able to sort the list without copying the nodes, changing it from an unsorted list into a sorted one. We can implement such a sort if we add two more methods to the IteratorI implementation:

  void insertBefore(T item); // add new element before current
  void remove();               // remove current

A given list may have more that one iterator active on it at one time, so the remove and insertBefore methods must be used with some care.

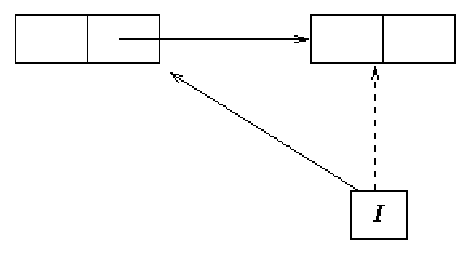
If an iterator must be able to remove the current element, then it must keep track of the element immediately before the current element. It will access the current element indirectly through the previous element.

If we use a dummy node which is always at the head of the list, this will work even in the boundary case where we delete the last element of the list.

When the list is empty, both head and last will point to the empty dummy node.