Species and Gene Evolution

PAM (Dayhoff) matrices

2022-10-06T09:00:00-05:00

The point accepted mutation (PAM) substitution model, also known as the Dayhoff substitution model, is an amino acid substitution model derived from empirical observation of mutations among closely related proteins. This venerable model was described in various volumes and supplements of the Atlas of Protein Sequence and Structure, with the most well-known version being published in the 1978 supplement by Dayhoff, Schwartz and Orcutt.

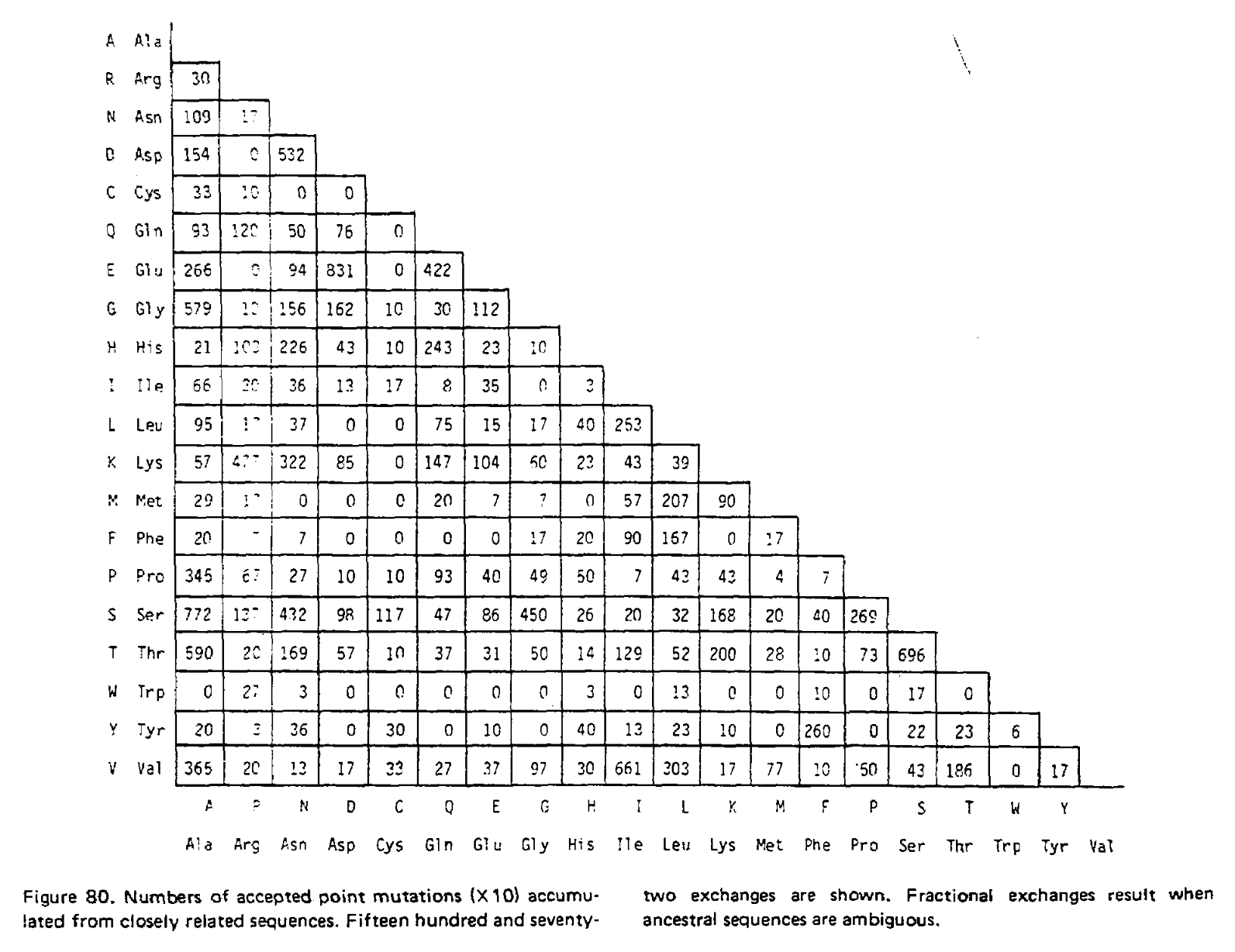
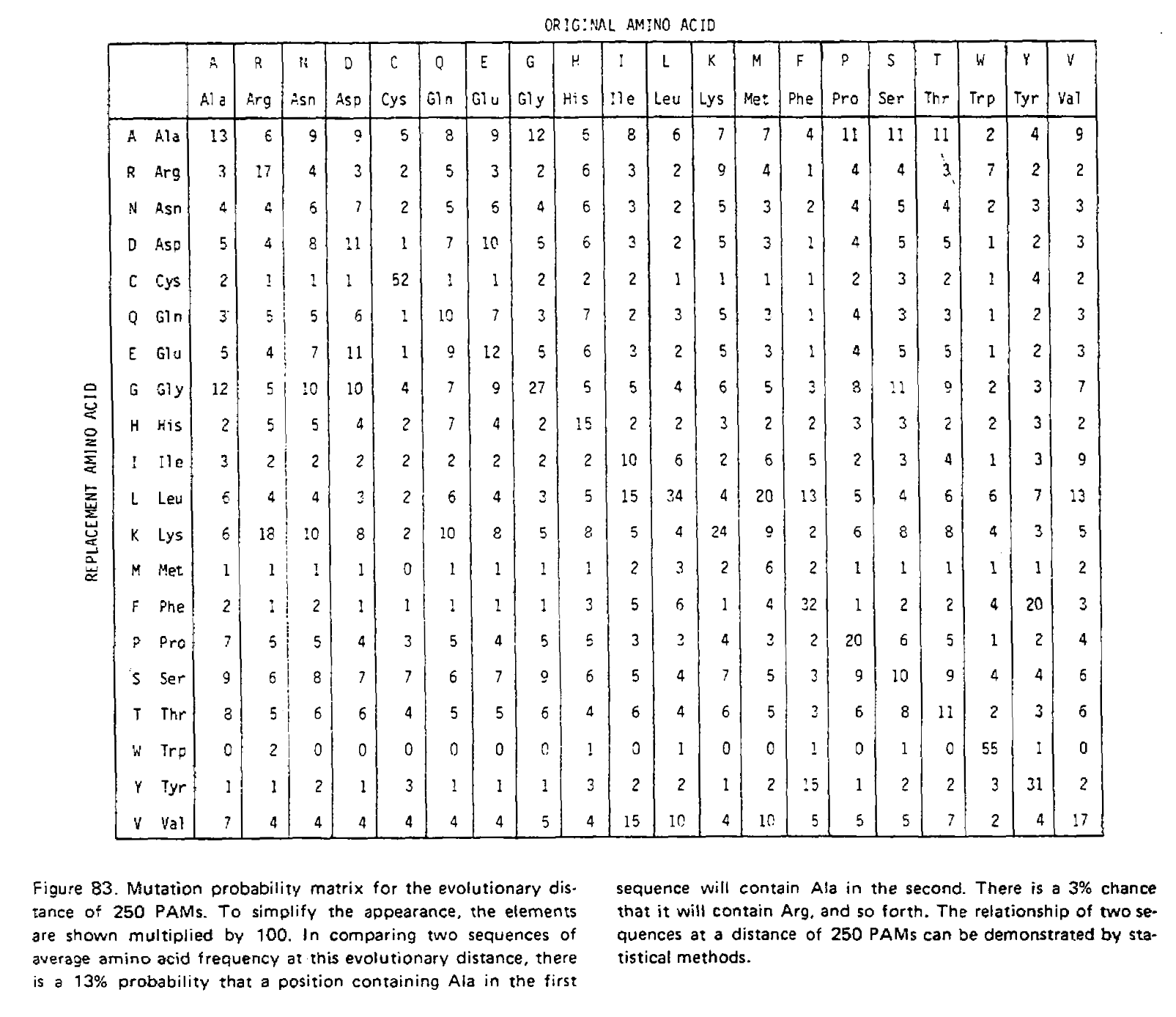
Since 1966, Dayhoff and her colleagues had been collecting and compiling protein sequences into their Atlas, and groups of closely related sequences from the Atlas were used as the basis for the PAM matrix. Where more than two sequences were in a group, phylogenetic trees were inferred along with ancestral sequences on each node of the tree, presumably using a method similar to the one published by Eck and Dayhoff in 1966. This method has been variously described as maximum parsimony (e.g. in Zhang and Nei 1996) or minimum evolution (e.g. in Edwards 1996).

Maximum parsimony (MP) methods optimize for the smallest possible number of mutations; for a given tree there will be a minimum number of mutations required to explain the known sequences, and MP methods attempt to find the tree with the smallest minimum number of mutations.

Each branch of a tree is associated with a pair of sequences, one at either end of the branch. These pairs of sequences were extracted from each tree. For each pair of sequences either from a tree or from the groups of size two, if there were two different amino acids at a given position it was assumed that a single mutation - a PAM - had occured, directly changing the amino acid of one of the sequences to the amino acid of the other sequence. This assumption is justified on the basis that sequences will be closely related enough that only one or zero mutations are likely to have occured at each site within these pairs. Models of sequence evolution making this assumption are commonly known as infinite-sites models (e.g. in Tajima 1996). If this assumption holds, then the vector of counts of mutations from one amino acid to the other nineteen amino acids should be proportional to the rates of transition from that one amino acid to the other nineteen, albeit with some sampling error.

In the 1978 version of the matrix, 71 groups were identified containing 1,572 mutations in total. Using the above procedure, point accepted mutations occuring in this dataset were counted and recorded in a matrix called A. This is a triangular matrix because the process is assumed to be reversible conditional on there being a mutation from the initial state; the probability of a mutation from state X to state Y, conditional on there being a mutation from state X to anything else, is the same as a mutation from Y to X conditional on there being a mutation from Y to anything else. Here is the count matrix:

We want to transform this matrix into a transition probability matrix M. Given some alphabet of states C, that matrix gives us the probability of a particular end state C_i (in this case, a particular amino acid) given an initial state C_j and some duration of time t, which we can write as M_ij = P(C_i|C_j, t). For the case where a mutation has definitely occured and i is different from j, we can express this as the joint probability P(C_i, i ≠ j|C_j, t), which will correspond to the off-diagonal elements of M. Following the chain rule, we can decompose this joint probability into P(C_i|C_j, i ≠ j, t)P(i ≠ j|C_j, t). When t is small enough that the infinite sites assumption is reasonable, then the probability of C_i conditioned on i ≠ j will not depend on t, and this formulation can be approximated as P(C_i|C_j, i ≠ j)P(i ≠ j|C_j, t).

We can estimate P(C_i|C_j, i ≠ j) from the symmetric version of the above triangular matrix of counts, by transforming the count of j to i mutations A_ij into a proportion by dividing this count by the total number of all mutations starting with j, or Σ_iA_ij. To compute the probability of any mutation P(i ≠ j|C_j, t), first the relative “mutability” m of each amino acid was calculated, a value which is proportional to (but not equal to) that probability when t is small enough that multiple mutations are unlikely. Put another way, m_j is approximately proportional to P(i ≠ j|C_j, t) for any small value of t. To derive the PAM/Dayhoff matrix, mutability was estimated as the number of mutations involving C_j relative to the overall occurance of C_j across all sequences. This mutability score was normalized so that the mutability of alanine equaled 100, an arbitrary choice given m is only proportional to the desired probabilities.

Finally, for each amino acid, an overall scaling factor λ was used to scale m_j from a relative value to the probability of mutation given 1 unit of time, i.e. λm_j = P(i ≠ j|C_j, t = 1). We can now calculate the off-diagonal values (where i ≠ j) of the transition probability matrix for t = 1 as:

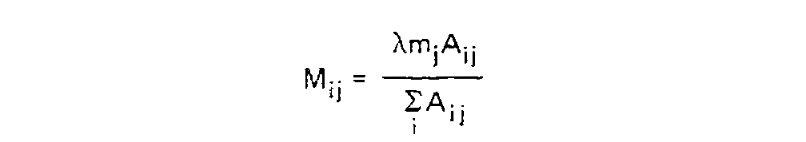
This scaling factor was calculated to set the unconditional mutation probability, that is P(i ≠ j), to equal 0.01 mutations per site, or equivalently equal 1 mutation for every 100 sites, given the resulting substitution matrix and an underlying amino acid frequency distribution. As a result, 1 unit of time is equal to the amount of time in which we expect 0.01 mutations to occur per site, which is called 1 PAM unit. Since whether or not a mutation has occured is a binary choice, the diagonal matrix values for 1 PAM unit, which correspond to P(i = j|C_j, t = 1), are equal to 1 - P(i ≠ j|C_j, t = 1) or:

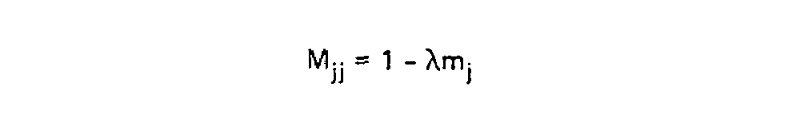
Using these two formulae, Dayhoff and colleagues calculated the entire transition probability matrix for 1 PAM unit:

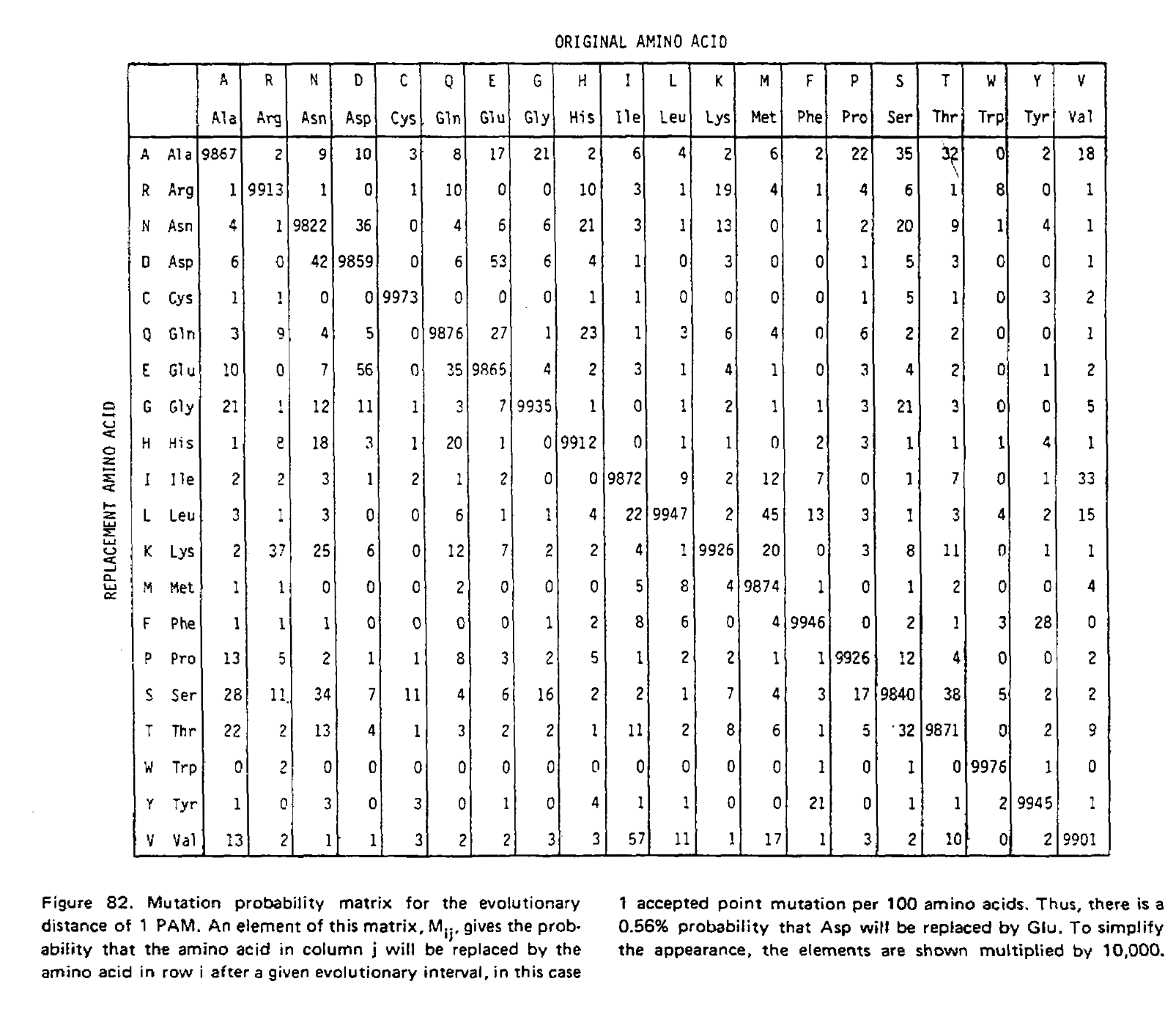
However, it is unlikely we are analyzing sequences exactly 1 PAM unit apart. As such we need to derive matrices for greater values of t, and in their 1978 supplement Dayhoff and colleagues derived the PAM250 matrix. This was done using matrix multiplication because at larger distances, multiple substitutions become much more likely. To illustrate the use of matrix multiplication to derive PAMn matrices, let’s consider a toy example with just three states; red, green and blue. Here is our transition probability matrix for one time unit:

	red	green	blue
red	0.95	0.08	0.01
green	0.04	0.84	0.04
blue	0.01	0.08	0.95

While modern phylogenetic methods treat evolution as a continuous-time Markov chain (CTMC) where each time step is infinitesimally small, in this case I will approximate evolution as a discrete-time Markov chain (DTMC) with time steps of 1 time unit as it is easier to explain.

After one time step, there is only one way a state can remain unchanged; no mutation must have occured. But after two time steps there is another possibility; a mutation occured at the first time step, and was reversed in the second.

For example, if the state is red at the start and end of the process, it could have remained unchanged over two time steps, but could also have mutated to green in the first time step and back to red, or to blue and back. We therefore need to sum over these possibilities to get the probability of remaining red over two time units. We calculate this sum as M₁₁×M₁₁ + M₁₂×M₂₁ + M₁₃×M₃₁ = 0.95×0.95 + 0.04×0.08 + 0.01×0.01 = 0.9058. The same logic applies to every other entry in our matrix, and we can use it to create a the transition probability matrix for two time units:

	red	green	blue
red	0.9058	0.1440	0.0222
green	0.0720	0.7120	0.0720
blue	0.0222	0.1440	0.9058

We have just performed matrix multiplication, calculating M×M=M²! We could multiply the resulting matrix by M again to get M³, the transition probability matrix for three time units. The PAMn matrices were calculated this way, for example the PAM250 matrix:

Notice how the transition probabilities get “flatter” the more time has passed. Given an infinite amount of time, each column would have an identical set of probabilities; the final amino acid would be completely independent of the initial amino acid, and the log-odds scores calculated from these transition probabilities would be identical to the non-homologous log-odds scores.

COMP571 (Fall 2022)

2022-08-22T09:00:00-05:00

Important note: The information contained in the course syllabus, other than the absence policies, may be subject to change with reasonable advance notice, as deemed appropriate by the instructor.

Who

Instructor:

Huw A. Ogilvie
hao3@rice.edu

TAs:

Jared Slone
js201@rice.edu

Where and when

Lectures will be held in Maxfield Hall 252, on Mondays and Wednesdays, between 4:00–5:15 PM. All lectures will be delivered in-person and, without a reasonable excuse, attendence is expected. One scheduled office hour will be held on Zoom, at a time to be determined based on scheduling conflicts, and attendance by the whole class is encouraged so that everyone can benefit from the discussion. Office hours will not be recorded. Individual appointments outside this time are welcome.

Distribution of class materials and submission of assignments and projects will be conducted via Canvas. Slack will be used for coordination and communication around group projects.

Intended audience

The students who should take COMP571 are generally studying computer science, biology or genomics, and wish to learn how to apply algorithms and statistical models to important problems in biology and genomics.

Course objectives and learning outcomes

The primary objective of the course is to teach the theory behind methods in biological sequence analysis, including sequence alignment, sequence motifs, and phylogenetic tree reconstruction. By the end of the course, students are expected to understand and be able to write basic implementations of the algorithms which power those methods.

Course materials

The main material for this course will be lectures and the course blog. That said, Statistics for Biology and Health by Ewens & Grant is a good resource and a PDF copy should be accessible here or through the Fondren Library.

Software for the course

Algorithms and statistics will be demonstrated using Python. Assignments and projects will require some Python coding. R may be used for some demonstrations (because it is nice for data visualization) but not for assessment.

The NumPy and SciPy libraries for scientific computing will be used with Python. To install these libraries, first install the latest official distribution of Python 3. This can be downloaded for macOS or for Windows from Python.org, and should already be included with your operating system if you are using Linux.

Then simply use the Python package manage pip to install NumPy and SciPy from the command line, by running pip3 install numpy scipy.

Schedule and assessment

The course is organized around five themes~~, and there will be a corresponding theory-based homework assignment for each one~~;

Substitution models for gapless alignments
Global alignment, local alignment, and BLAST
Hidden Markov Models and transmembrane domain identification
Sankoff’s and hill climbing algorithms
Phylogenetic likelihood and coalescent theory

Assignments should be completed individually, copying answers without attribution from other sources including other students will be considered plagiarism.

In addition to these assignments, each student will have to complete one project of implementing a novel or existing statistical model, applying it to a public data set, and writing up the results in the style of a scientific paper. The statistical model should be relevant to one (or more) of the course themes. Projects will be designed by groups of 3–5 students, but the implementation, application and write up will be individual. Copying and pasting code or your report (in part or in whole) without attribution from other sources including other students will be considered plagiarism. Project code and reports will be due on December 2nd. A design document will be due on November 4th before the project due date which will be completed and submitted by the group rather than individually.

The below schedule may change subject to Rice University policy

Monday’s date	Monday’s lecture	Wednesday’s lecture	Homework
08/22/22	Introduction	Central dogma and gene models
08/29/22	canceled	canceled
09/05/22	Labor Day, no scheduled classes	Margaret Dayhoff’s Atlas¹
09/12/22	Homology testing using log-odds²	Global alignment²
09/19/22	Local alignment²	BLAST (gapless phase)²
09/26/22	BLAST (gapped phase)²	Hidden Markov models³	#1 issued
10/03/22	Viterbi algorithm³	Forward algorithm³	#1 due
10/10/22	Midterm recess, no scheduled classes	Backward algorithm³
10/17/22	canceled	Baum-Welch algorithm
10/24/22	Phylogenetic trees⁴	Hill climbing⁴	#2 issued
10/31/22	The Felsenstein zone⁴	Time-reversible models of evolution⁵	#2 due
11/07/22	Felsenstein’s pruning algorithm⁵	Wright–Fisher model⁵
11/14/22	Kingman’s coalescent⁵	Bayesian phylogenetic inference
11/21/22	Metropolis algorithm	Thanksgiving recess, no scheduled classes	#3 issued
11/28/22	Buffer	Buffer	#3 due
12/05/22	Scheduled classes finished	Scheduled classes finished

Each row in the above table lists the lecture topics, homework and project milestones for the week beginning on the specified Monday and ending the following Sunday. Superscript numbers refer to the theme(s) for that day’s class or midterm. Assignments will be issued before midnight on the Monday at the start of the week. Assignments will also be due before midnight on Fridays.

Project reports

The goal of the project design document is to enable your instructor and TA to provide feedback before you spend a lot of time implementing the required code. It is not intended to be very formal like a typical grant application or software requirement specification. It should describe the dataset(s) and method(s) you plan on using and implementing, and the rationale behind why the dataset(s) and method(s) are appropriate for the problem at hand, in sufficient detail for your instructor and TA to understand your approach.

I (Huw) would expect this to be approximately 2 pages in length, but it may be longer if that’s required for sufficient explanation. If adding figures and tables improves the clarity of your proposal, by all means include them. You should include references, but the formatting of the document and citation style is up to you.

Grade policies

Attendance: 5%
Homework assignments: 15% each
Project design document: 10%
Project implementation: 15%
Project report: 25%

Assignments or projects submitted late with a strong and valid excuse will be accepted without penalty. The strength and validity of excuses will be solely the instructor’s purview. Without a strong and valid excuse, the final course percentage will be reduced by 2% for each day any submission is late, up to the contribution of that submission to the final percentage. For example if submitted homework is given a mark of 70%, it contributes 70% × 20% = 14% to the final percentage.

No assignments or projects will be accepted after the end of the semester on Tuesday, December 13, 2022. In exceptional circumstances, if a student is unable to complete an assignment or project before the semester ends, the final percentage will be calculated by scaling the assessment which that student has completed. Again, this will be solely within the instructor’s purview.

Absence policies

Please let your instructor know if you are going to be absent from lectures and why. In-person lecture attendence is expected without a reasonable excuse. A non-exhaustive list of reasonable excuses includes illness, COVID exposure, time-sensitive experiments, or conference/workshop commitments.

Rice Honor Code

In this course, all students will be held to the standards of the Rice Honor Code, a code that you pledged to honor when you matriculated at this institution. If you are unfamiliar with the details of this code and how it is administered, you should consult the Honor System Handbook at http://honor.rice.edu/honor-system-handbook/. This handbook outlines the University’s expectations for the integrity of your academic work, the procedures for resolving alleged violations of those expectations, and the rights and responsibilities of students and faculty members throughout the process.

Students with a disability

If you have a documented disability or other condition that may affect academic performance you should: 1) make sure this documentation is on file with Disability Support Services (Allen Center, Room 111 / adarice@rice.edu / x5841) to determine the accommodations you need; and 2) talk with me to discuss your accommodation needs.

Backward algorithm

2020-10-23T05:00:00-05:00

Like the forward algorithm, we can use the backward algorithm to calculate the marginal likelihood of a hidden Markov model (HMM). Also like the forward algorithm, the backward algorithm is an instance of dynamic programming where the intermediate values are probabilities.

Recall the forward matrix values can be specified as:

f_k,i = P(x_1..i,π_i=k|M)

That is, the forward matrix contains log probabilities for the sequence up to the i^th position, and the state at that position being k. These log probabilities are not conditional on the previous states, instead they are marginalizing over the hidden state path leading up to k,i.

In contrast, the backward matrix contains log probabilities for the sequence after the i^th position, marginalized over the path, but conditional on the hidden state being k at i:

b_k,i = P(x_i+1..n|π_i=k,M)

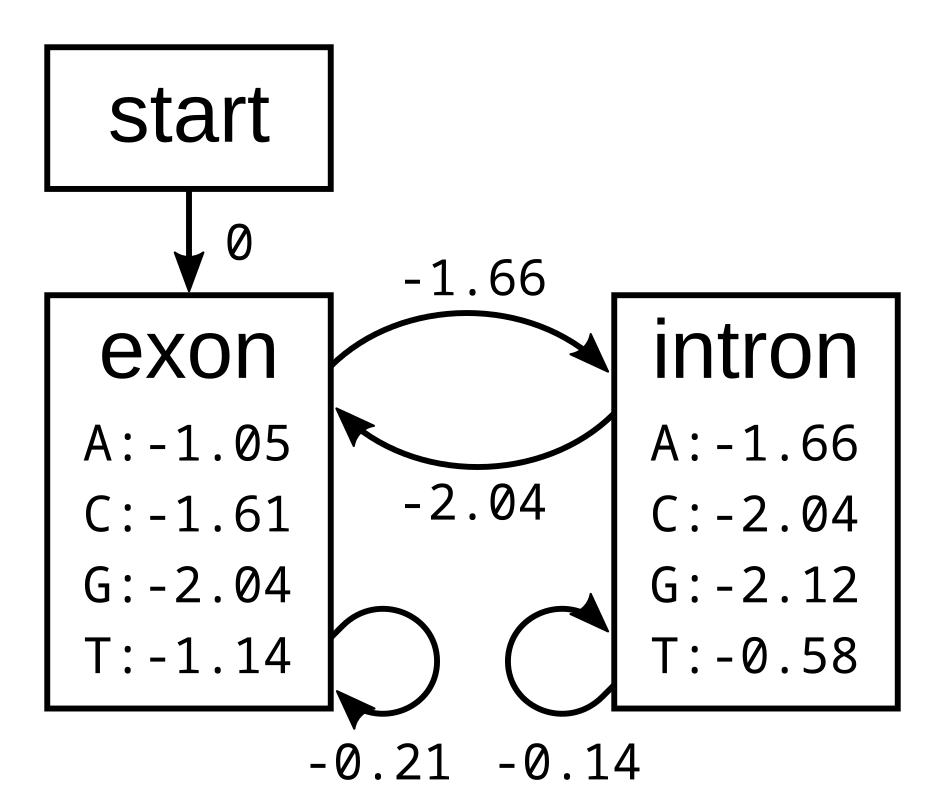
To demonstrate the backward algorithm, we will use the same example sequence CGGTTT and the same HMM as for the Viterbi and forward algorithm. Here again is the HMM with log emission and transmission probabilities:

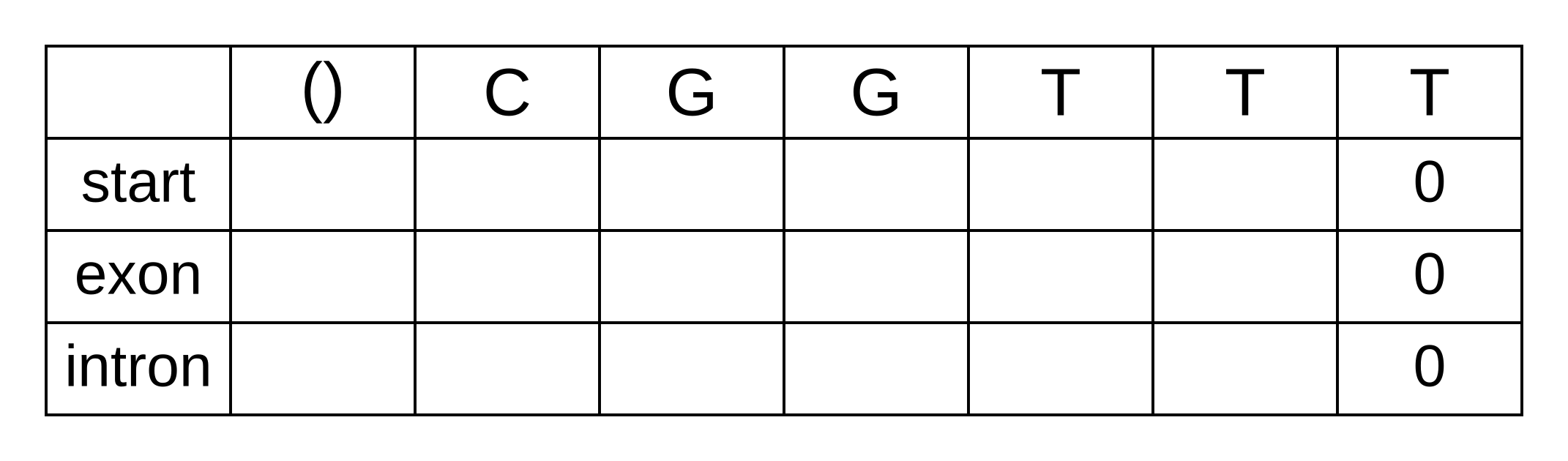
To calculate the backward probabilities, initialize a matrix b of the same dimensions as the corresponding Viterbi or forward matrices. The conditional probability of an empty sequence after the last position is 100% (or a log probability of zero) regardless of the state at the last position, so fill in zeros for all states at the last column:

To calculate the backward probabilities for a given hidden state k at the second-to-last position i = n - 1, gather the following log probabilities for each hidden state k’ at position i + 1 = n:

the hidden state transition probability t_k,k’ from state k at i to state k’ at i + 1
the emission probability e_k’,i+1 of the observed state (character) at i + 1 given k’
the probability b_k’,i+1 of the sequence after i + 1 given state k’ at i + 1

The sum of the above log probabilities gives us the log joint probability of the sequence from position i + 1 onwards and the hidden state at i + 1 being k’, conditional on the hidden state at i being k. The log sum of exponentials (LSE) of the log joint probabilities for each value of k’ marginalizes over the hidden state at i + 1, therefore the result of the LSE function is the log conditional probability of the sequence alone from i + 1.

We do not have to consider transitions to the start state, because (1) these transitions are not allowed by the model, and (2) there are no emission probabilities associated with the start state. The only valid transition from the start state at the second-to-last position is to an exon state, so its log probability will be:

b_start,n-1 = t_start,exon + e_exon,n + b_exon,n = 0 + -1.14 + 0 = -1.14

For the exon state at n - 1, we have to consider transitions to the exon or intron states at n. Its log probability will be the LSE of:

t_exon,exon + e_exon,n + b_exon,n = -0.21 + -1.14 + 0 = -1.35
t_exon,intron + e_intron,n + b_intron,n = -1.66 + -0.58 + 0 = -2.24

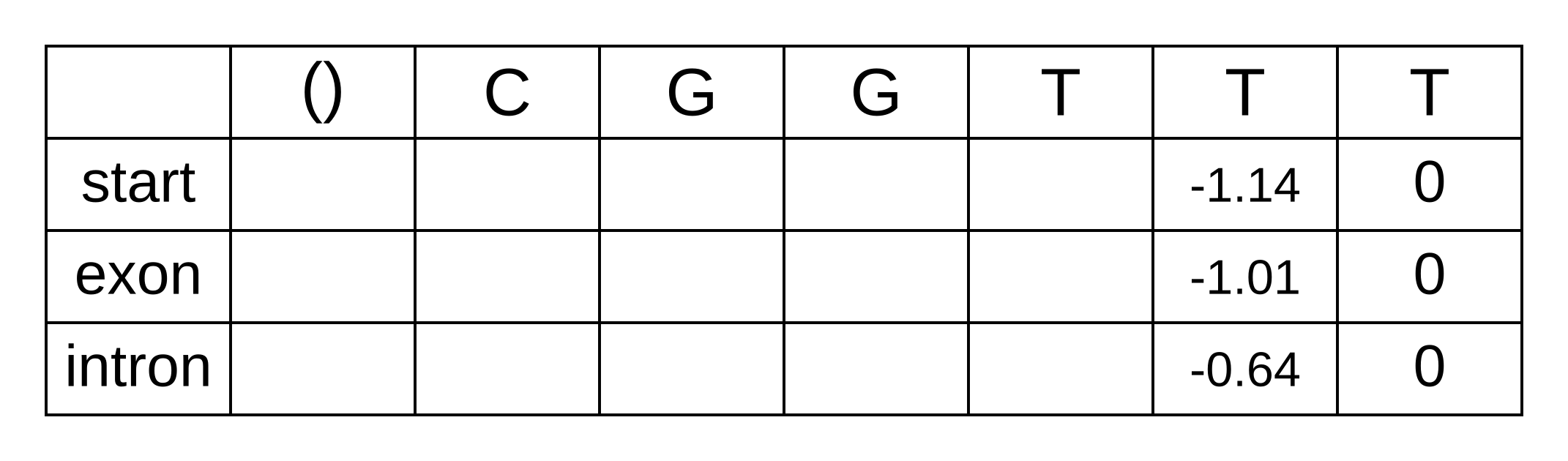
The LSE of -1.35 and -2.24 is -1.01. and and For the intron state at n - 1 the log-probabilities to marginalize over are:

t_intron,exon + e_exon,n + b_exon,n = -2.04 + -1.14 + 0 = -3.18
t_{intron,intron} + e_intron,n + b_intron,n = -0.14 + -0.58 + 0 = -0.72

The LSE of -3.18 and -0.72 is -0.64. We can now update the backward matrix with the second-to-last column:

The third-to-last position is similar. For the start state we only have consider the one transition permitted by the model:

b_start,n-2 = t_start,exon + e_{exon,n - 1} + b_{exon,n - 1} = 0 + -1.14 + -1.01 = -2.15

For the exon state at n - 2, the same as for n - 1, we have to consider two log-probabilities:

t_exon,exon + e_{exon,n - 1} + b_{exon,n - 1} = -0.21 + -1.14 + -1.01 = -2.36
t_exon,intron + e_{intron,n - 1} + b_{intron,n - 1} = -1.66 + -0.58 + -0.64 = -2.88

The LSE for these log probabilities is -1.89. Likewise for the intron state at n - 2:

t_intron,exon + e_{exon,n - 1} + b_{exon,n - 1} = -2.04 + -1.14 + -1.01 = -4.19
t_{intron,intron} + e_{intron,n - 1} + b_{intron,n - 1} = -0.14 + -0.58 + -0.64 = -1.36

And the LSE for these log probabilities is -1.30. We can now fill in the third-to-last column of the matrix, and every column going back to the first column of the matrix:

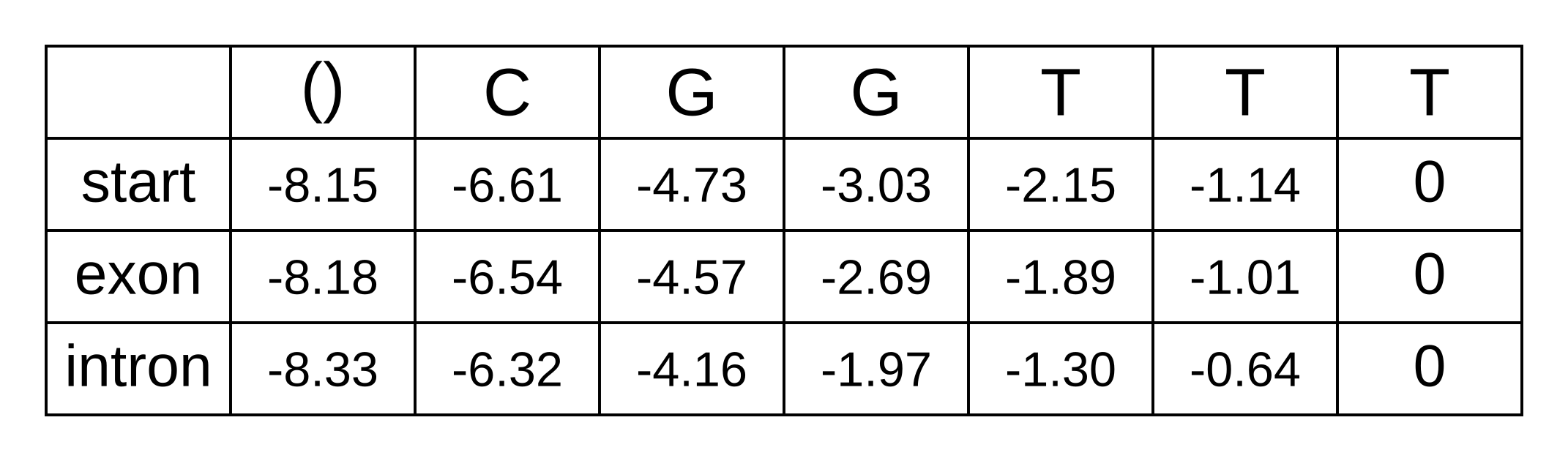
The first column of the matrix represents the beginning of the sequence, before any characters have been observed. The only valid hidden state for the beginning is the start state, and therefore the log probability b_start,0 = logP(x_1..n|π₀=start,M) can be simplified to logP(x_1..n|M). Because the sequence from 1 to n is the entire sequence, it can be further simplified to logP(x|M). In other words, this value is our log marginal likelihood! Reassuringly, it is the exact same value we previously derived using the forward algorithm.

Why do we need two dynamic programming algorithms to compute the marginal likelihood? We don’t! But by combining probabilities from the two matrices, we can derive the posterior probability of each hidden state k at each position i, marginalized over all paths through k at i. How this this work? If two variables a and b are independent, their joint probability P(a,b) is simply the product of their probabilities P(a) × P(b). Under our model, the two segments of the sequence x_1..i and x_i+1..n are dependent on paths of hidden states. However, the because we are using a hidden Markov model, the path and sequence from i onwards depends only on the particular hidden state at i. This is because the transition probabilities are Markovian so they depend only on the previous hidden state, and because the emission probabilities depend only on the current hidden state. As a result, while P(x_1..i|M) and P(x_i+1..n|M) are not independent, P(x_1..i|π_i=k,M) and P(x_i+1..n|π_i=k,M) are! Therefore (dropping the model term M for space and clarity):

P(x_1..i|π_i=k) × P(x_i+1..n|π_i=k) × P(π_i=k) = P(x_1..i, x_{i + 1..n}|π_i=k) × P(π_i=k) = P(x|π_i=k) × P(π_i=k)

Using the transitivity of equivalence, the product on the left hand side above must equal the product on the right hand side above. By applying the chain rule, it can also be shown that both are equal to the product on the right hand side below:

P(x|π_i=k) × P(π_i=k) = P(x_1..i|π_i=k) × P(x_i+1..n|π_i=k) × P(π_i=k) = P(x_1..i, π_i=k) × P(x_i+1..n|π_i=k)

Or in log space:

logP(x|π_i=k) + logP(π_i=k) = logP(x_1..i, π_i=k) + logP(x_i+1..n|π_i=k)

Notice that the sum on the right hand side above corresponds exactly to f_k,i + b_k,i! Now using Bayes rule, and remembering that b_start,0 equals the log marginal likelihood, we can calculate the log posterior probability of π_i=k:

logP(π_i=k|x) = logP(x|π_i=k) + logP(π_i=k) - logP(x) = logP(x_1..i, π_i=k) + logP(x_i+1..n|π_i=k) - logP(x) = f_k,i + b_k,i - b_0,start

And now we can now “decode” our posterior distribution of hidden states. We need to refer back to the previously calculated forward matrix, shown below.

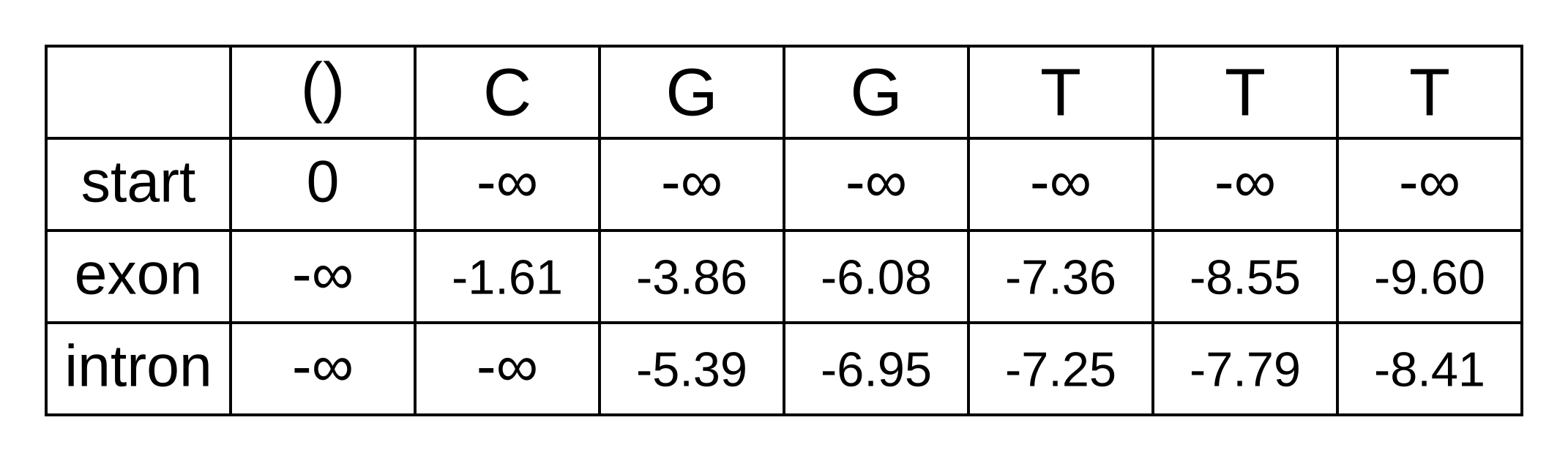
As an example, let’s solve the log marginal probability that the hidden state of the fourth character is an exon:

logP(π₄=exon|x,M) = f_exon,4 + b_exon,4 - b_start,0 = -1.89 + -7.36 - -8.15 = -1.1

The marginal probability is exp(-1.1) = 33%. Since we only have two states, the probability of the intron state should be 67%, but let’s double check to make sure:

logP(π₄=intron|x,M) = f_intron,4 + b_intron,4 - b_start,0 = -1.30 + -7.25 - -8.15 = -0.4

Since exp(-0.4) = 67%, it seems like we are on the right track! The posterior probabilities can be shown as a graph in order to clearly communicate your results:

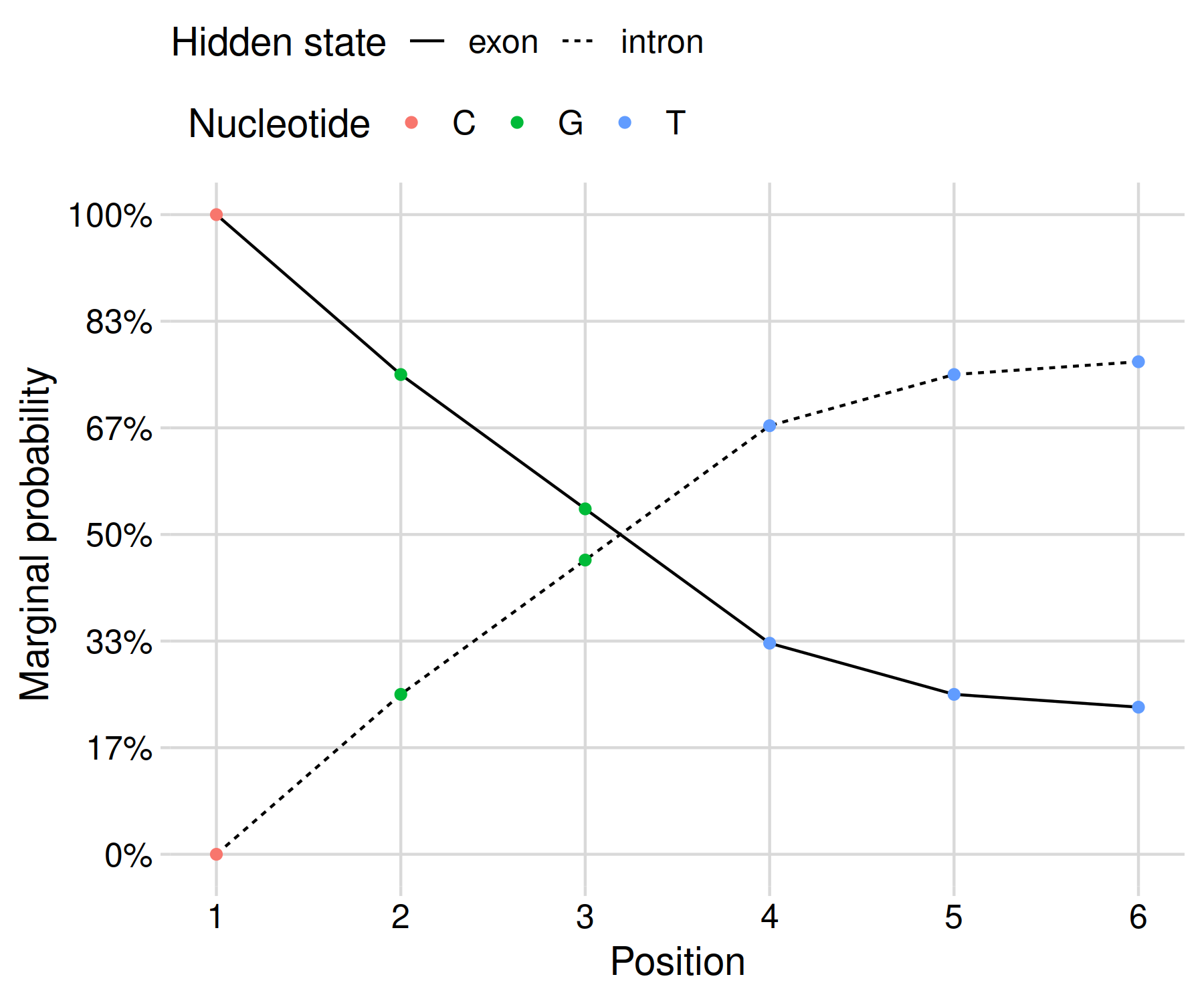
This gives us a result that reflects the uncertainty of our inference given the limited data at hand. In my opinion, this presentation is more honest than the black-and-white maximum a posteriori result derived using Viterbi’s algorithm.

For another perspective on the backward algorithm, consult lesson 10.11 of Bioinformatics Algorithms by Compeau and Pevzner.

Forward algorithm

2020-10-23T01:00:00-05:00

The Viterbi algorithm identifies a single path of hidden Markov model (HMM) states. This is the path which maximizes the joint probability of the observed data (e.g. a nucleotide or amino acid sequence) and the hidden states, given the HMM (including transition and emission frequencies).

Maybe this path is almost certainly correct, but it also might represent one of many plausible paths. Putting things quantitatively, the Viterbi result might have a 99.9% probability of being the true¹ path, or a 0.1% probability. It would be useful to know these probabilities in order to understand when our results obtained from the Viterbi algorithm are reliable.

Recall that the joint probability is P(π,x|M) where (in the context of biological sequence analysis) x is the biological sequence, π is the state path, and M is the HMM. Following the chain rule, this is equivalent to P(x|π,M) × P(π|M). The maximum joint probability returned by the Viterbi algorithm is therefore the product of the likelihood of the sequence given the state path, and the prior probability of the state path! Previously I have described the product of the likelihood and prior as the unnormalized posterior probability. The parameter values which maximize that product, and therefore the state path returned by the Viterbi algorithm, is often known as the “maximum a posteriori” solution.

The posterior probability is obtained by dividing the unnormalized posterior probability (which can be obtained using the Viterbi algorithm) by the marginal likelihood. The marginal likelihood can be calculated using the forward algorithm.

The intermediate probabilities calculated using the Viterbi algorithm are the probabilities of a state path π and a biological sequence x up to some step i: P(π_1..i,x_1..i|M). The intermediate probabilities calculated using the forward algorithm are similar but marginalize over the state path up to step i: P(π_i,x_1..i|M). Put another way, the probability is for the state at position i integrated over the path followed to that state.

This marginalization is achieved by summing over the choices made at each step. When calculating probabilities, summing typically achieves the result of X or Y (e.g., a high OR low path), whereas a product typically achieves the result of X and Y (e.g. a high then low path).

Just as for the Viterbi algorithm, it is sensible to work in log space to avoid numerical underflows and loss of precision. As an alternative to working in log space while still avoiding those errors, the marginal probabilities of all states at any position along the sequence can be rescaled (see section 3.6 of Biological Sequence Analysis). However if those marginal probabilities are very different in magnitude, there can still be numerical errors even with rescaling, so from here on we will work in log space.

As an example we will use the forward algorithm to calculate the log marginal likelihood of the sequence CGGTTT and HMM used in the Viterbi example. Initialize an empty forward matrix with the first row and column filled in, same as the Viterbi matrix:

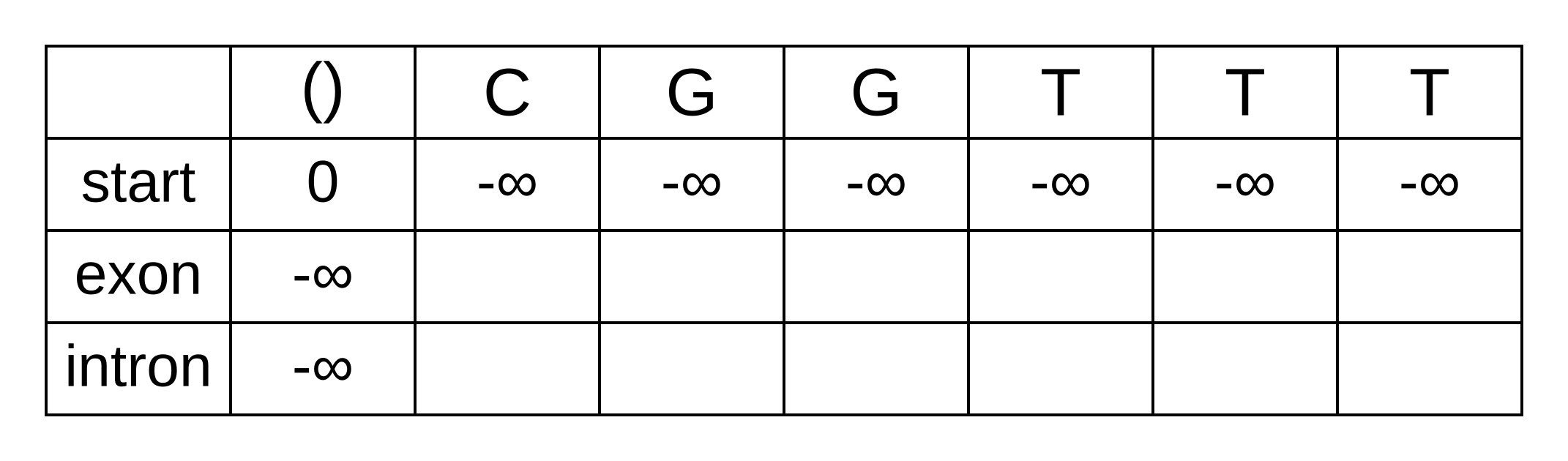
To calculate the log marginal probability of a particular state at some position of the sequence, we need to sum over the probabilies that lead from any previous state to the particular state at that position. These are not the log-probabilities being summed over, but the actual zero to one probabilities. In log space, this requires logging the sum of exponentials of the log-probabilities, or LogSumExp (LSE) for short.

The only valid paths up to the second position of the sequence under our model are start-exon-exon and start-exon-intron, so the first three columns will be identical to the Viterbi matrix as no summation is required:

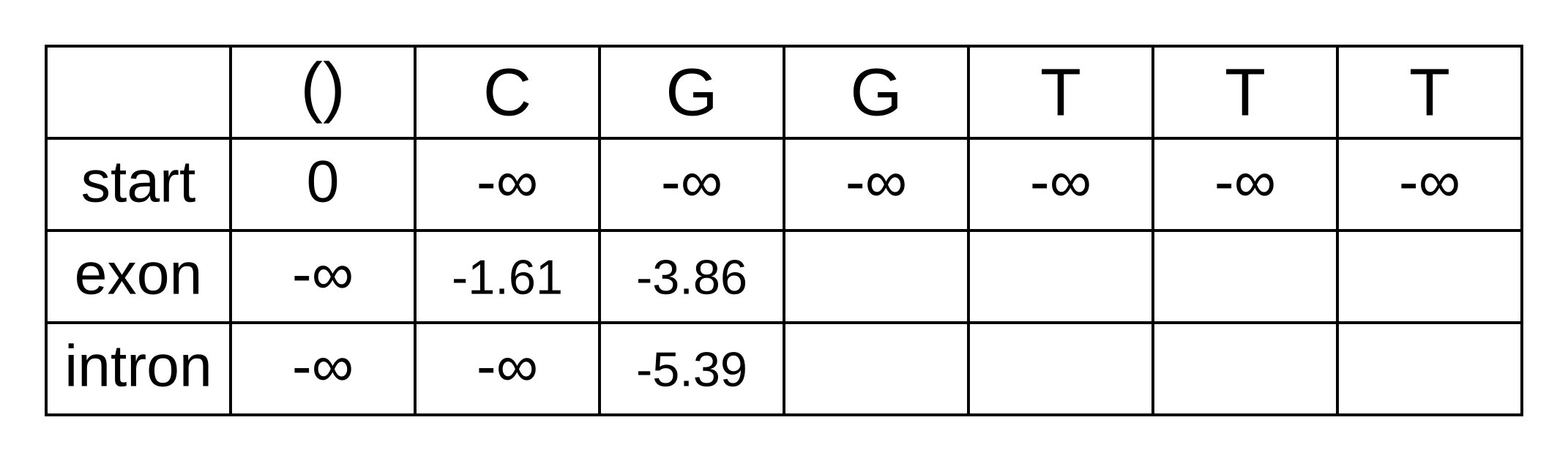
Because of the marginalization, there are no pointer arrows to add to the forward matrix. The third position (fourth column) is more interesting, as we have to marginalize over multiple log probabilities of the state at the previous position. For the exon state at the third position, these log probabilities are:

f_exon,2 + t_exon,exon + e_exon,3 = -3.86 + -0.21 + + -2.04 = -6.11
f_intron,2 + t_intron,exon + e_exon,3 = -5.39 + -2.04 + -2.04 = -9.47

The log marginal probability (to two decimal places) is therefore LSE(-6.11, -9.47) = log(exp(-6.11) + exp(-9.47)) = -6.08. This calculation can be performed in one step using the Python function scipy.special.logsumexp. To use this command scipy must be installed and the scipy.special subpackage must be imported. In fact, it should be performed in one step to avoid the aforementioned numerical errors.

The log probabilities to marginalize over for the intron state at the third position are:

f_exon,2 + t_exon,intron + e_intron,3 = -3.86 + -1.66 + -2.12 = -7.64
f_intron,2 + t_{intron,intron} + e_intron,3 = -5.39 + -0.14 + -2.12 = -7.65

The log marginal probability is therefore LSE(-7.64, -7.65) = log(exp(-7.64) + exp(-7.65)) = -6.95. The log marginal probabilities for each state at each position can be calculated the same way, and the completed forward matrix will be:

At the last position, we have the log marginal joint probability of the sequence and path over all paths that end in an exon state, and log marginal joint probability over all paths that end in an intron state. The LSE of these two log probabilities is therefore the log marginal likelihood of the model, because it marginalizes over all state paths, and equals to LSE(-9.60, -8.41) = log(exp(-9.60) + exp(-8.41)) = -8.15.

We previously calculated the log probability of the maximum a posteriori path as -9.79. The posterior probability is therefore exp(-9.79 - -8.15) = exp(-1.64) = 19.4%. The Viterbi result is very plausible (events with 19.4% probability occur all the time) but most likely wrong.

For more information see section 3.2 of Biological Sequence analysis by Durbin, Eddy, Krogh and Mitchison.

For another perspective on the forward algorithm, consult lesson 10.7 of Bioinformatics Algorithms by Compeau and Pevzner.

Such probabilities are conditioned on the model being correct. So more accurately, they are the probability of a parameter value being true if the model (e.g. an HMM) used for inference is also the model which generated the data. If the model is wrong, the probabilities can be quite spurious, see Yang and Zhu (2018). ↩

Viterbi algorithm

2020-10-22T09:00:00-05:00

The Viterbi algorithm is used to efficiently infer the most probable “path” of the unobserved random variable in an HMM. In the CpG islands case, this is the most probable combination of CG-rich and CG-poor states over the length of the sequence. In the splicing case, this the most probable structure of the gene in terms of exons and introns.

Conceptually easier than Viterbi would be the brute force solution of calculating the probability for all possible paths. However the number of possible paths for two states, as in the CpG island model, is 2ⁿ where n is the number of sites. For even a short sequence of 1000 nucleotides, this equates to 2¹⁰⁰⁰ paths, or approximately 10³⁰¹. This number is about 10²²¹ times larger than the number of atoms in the observable universe.

I will first demonstrate how the algorithm works using the following simple exon-intron model:

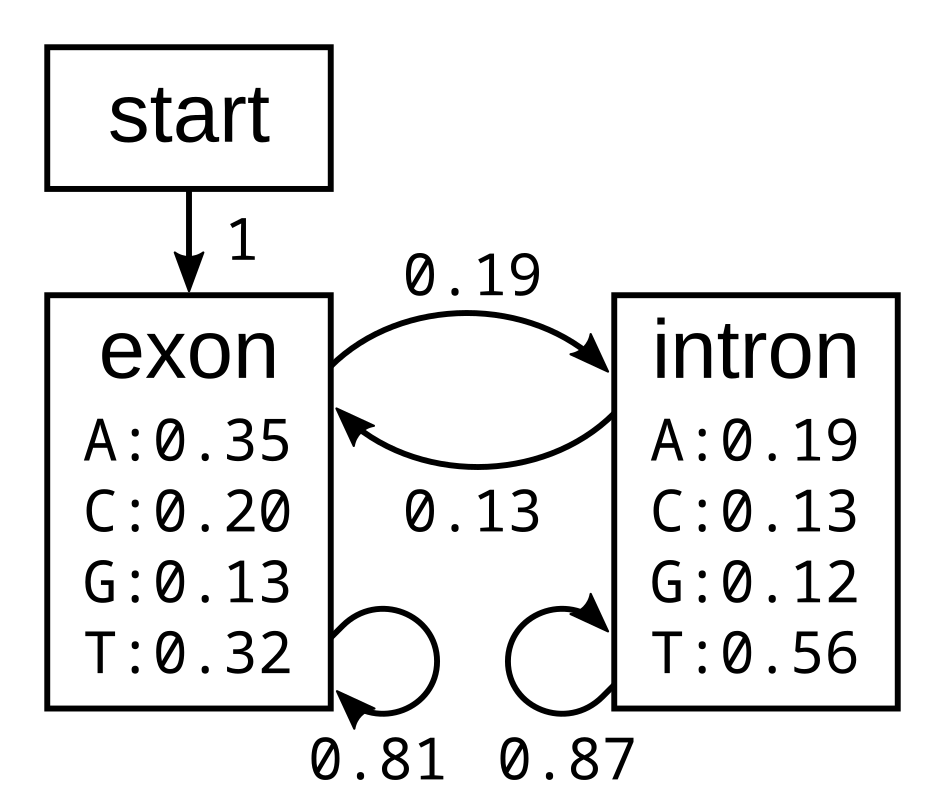
The probabilities of the model have the corresponding log-probabilities, to two decimal places:

Let’s apply this simple model to the toy sequence CGGTTT.

Draw up a table and fill in the probabilities of the states when the sequence is empty: 0 log-probability (100% probability) for being in the start state at the start of the sequence, and negative infinity (0% probability) for not being in the start state at the start of the sequence:

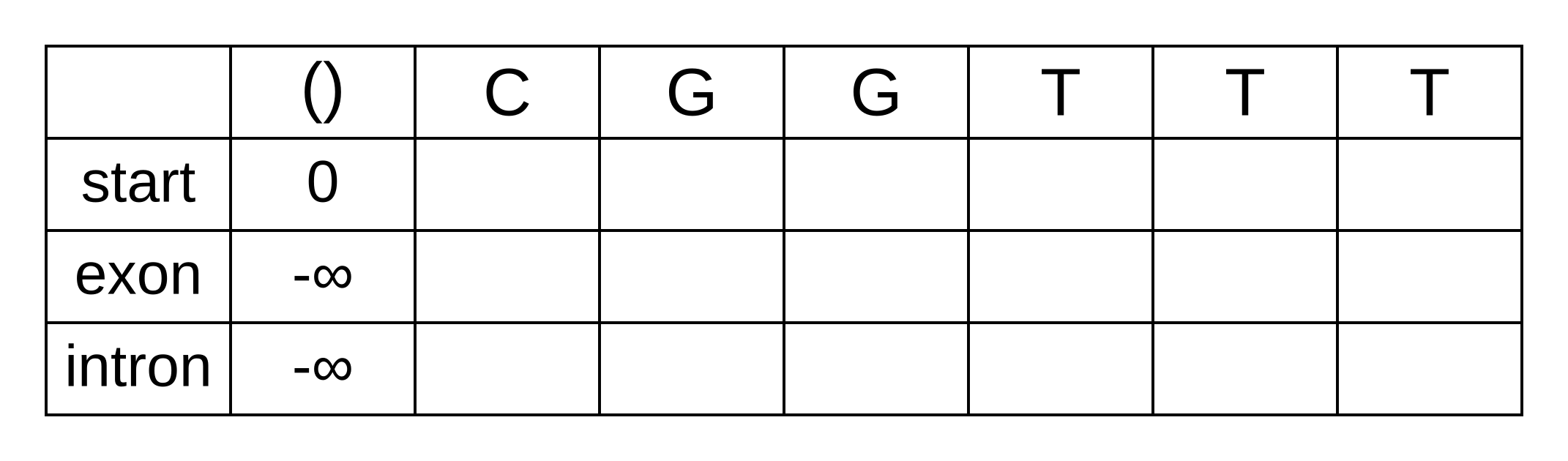
We will refer to every element of the matrix as v_k,i where k is the hidden state, and i is the position within the sequence. v_k,i is the maximum log joint probability of the sequence and any path up to i where the hidden state at i is k:

v_k,i = max_{path_1..i-1}(logP(seq_1..i, path_1..i-1, path_i = k)).

This log joint probability is equal to the maximum value of v_k’,i-1 where k’ is the hidden state at the previous position, plus the transition log-probability t_k’,k of transitioning from the state k’ to k, plus the emission log-probability e_k,i of the nucleotide (or amino acid for proteins) at i given k. We find this value by calculating this sum for every previous hidden state k’ and choosing the maximum.

The transition log probability from any state to the start state is -∞, so for any value of i from 1 onwards, v_start,i = -∞. Go ahead and fill those in to save time:

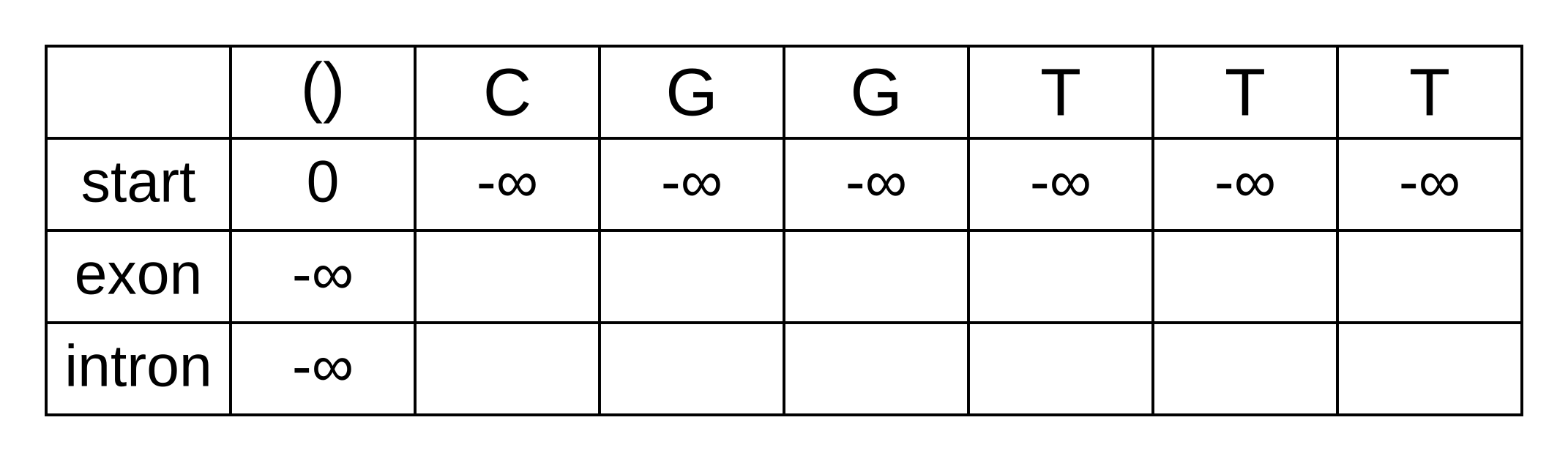
For the next element v_exon,1 we only have to consider the transition from the start state to the exon state, because that is the only transition permitted by the model. Even if we do the calculations for the other transitions, the results of those calculations will be negative infinities because the Viterbi probability of non-start states in the first column are negative infinities. The log-probability at v_exon,1 is therefore:

v_exon,1 = v_start,0 + t_start,exon + e_exon,1 = 0 + 0 + -1.61 = -1.61

The log-probability of v_intron,1 is negative infinity because the model does not permit the state at the first sequence position to be an intron. This can be effected computationally by setting the t_start,intron log-probability to negative infinity. Then regardless of the Viterbi and emission log-probabilities, the sum of v, t and e will be negative infinity.

Fill in both values for the first position of the sequence (or second column of the matrix), and add a pointer from the exon state to the start state:

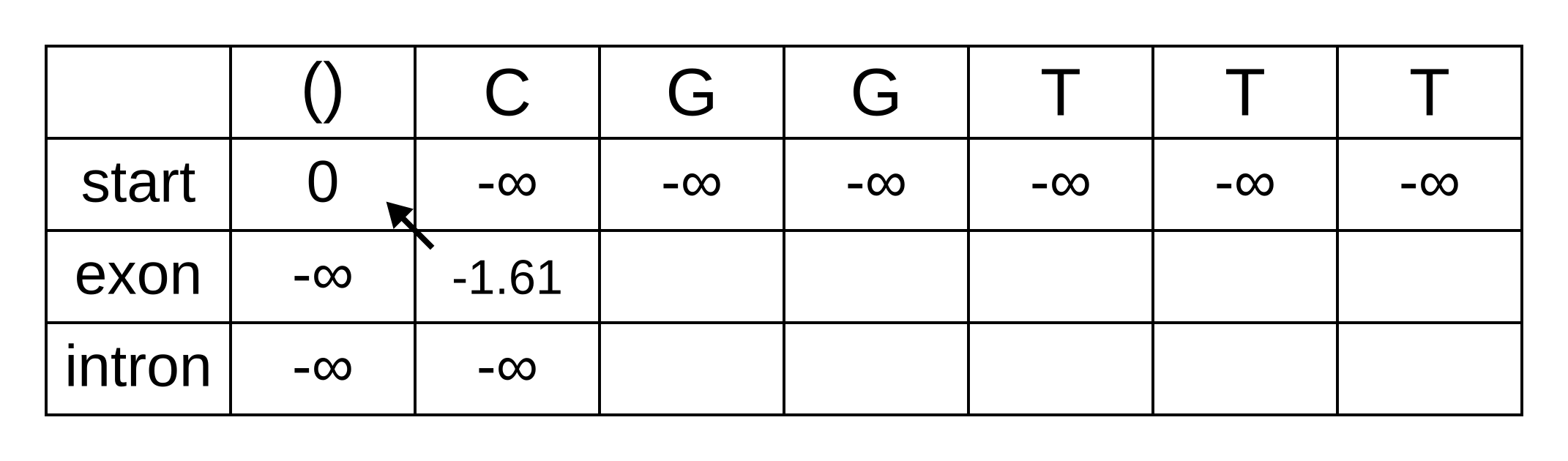
Once we get to v_exon,2, we only have to consider the exon to exon transition since the log-probabilities for the other states at the previous position are negative infinities. So this log-probability will be:

v_exon,2 = v_exon,1 + t_exon,exon + e_exon,2 = -1.61 + -0.21 + -2.04 = -3.86

And for the same reason to calculate v_intron,2 we only have to consider the exon to intron transition, and this log-probability will be:

v_intron,2 = v_exon,1 + t_exon,intron + e_intron,2 = -1.61 + -1.66 + -2.12 = -5.39

So fill on those values, and add pointers to the only permitted previous state, which is the exon state:

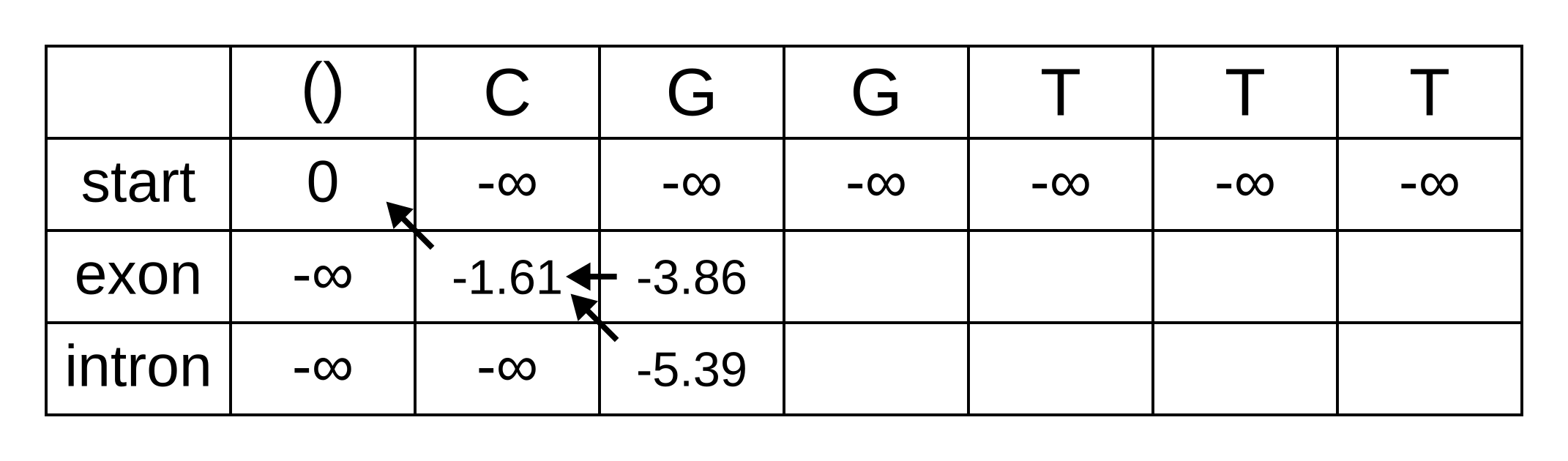
For the next position, we have to consider all transitions between intron or exon to intron or exon since both of those states have finite log-probabilities at the previous position. The log-probability of v_exon,3 will be the maximum of:

v_exon,2 + t_exon,exon + e_exon,3 = -3.86 + -0.21 + -2.04 = -6.11
v_intron,2 + t_intron,exon + e_exon,3 = -5.39 + -2.04 + -2.04 = -9.47

The previous hidden state that maximizes the Viterbi log-probability for the exon state at the third sequence position is therefore the exon state, and the maximum log-probability is -6.11. The log-probability of v_intron,3 will be the maximum of:

v_exon,2 + t_exon,intron + e_intron,3 = -3.86 + -1.66 + -2.12 = -7.64
v_intron,2 + t_{intron,intron} + e_intron,3 = -5.39 + -0.14 + -2.12 = -7.65

The previous hidden state that maximizes the Viterbi log-probability for the intron state at the third sequence position is therefore also the exon state, and the maximum log-probability is -7.64.

Fill in the maximum log-probabilities for each hidden state k, and also draw pointers to the previous hidden states corresponding to those maximum log-probabilities:

The rest of the matrix is filled in the same way as for the third position:

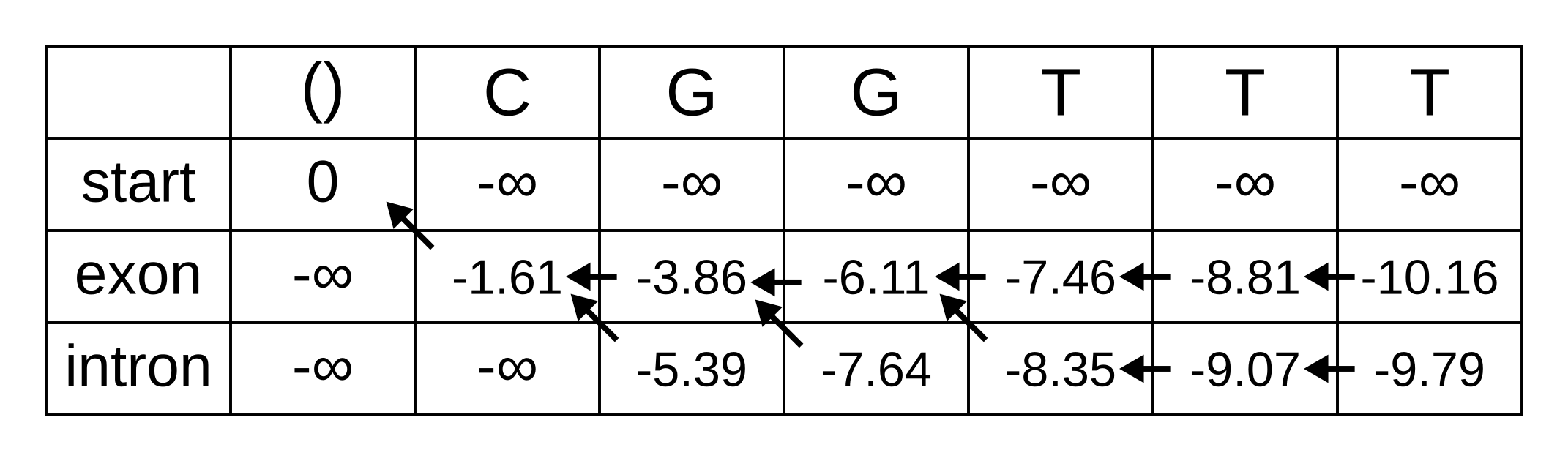
The maximum log joint probability of the sequence and path is the maximum out of v_k,L, where L is the length of the sequence. In other words, if we calculate the log joint probability

v_k,L = max_{path_1..L-1}(logP(seq_0..L, path_0..L-1, path_L = k)).

for every value of k, we can identify the maximum log joint probability unconditional on the value of k at L. The path is then reconstructed by following the pointers backwards from the maximum log joint probability. In our toy example, the maximum log joint probability is -9.79 and the path is:

Or, ignoring the start state, exon-exon-exon-intron-intron-intron.

The basic Viterbi algorithm has a number of important properties:

Its space and time complexity is O(Ln) and O(Ln²) respectively, where n is the number of states and L is the length of the sequence
It returns a point estimate rather than a probability distribution
Like Needleman–Wunsch or Smith–Waterman it is exact, so it is guaranteed to find the optimal¹ solution, unlike heuristic algorithms, and unlike an MCMC chain run for a finite number of steps²
The probability is the (log) joint probability of the entire sequence (e.g. nucleotides or amino acids) and the entire path of unobserved states. It is not identifying the most probable hidden state at each position, because it is not marginalizing over the hidden states at other positions.

If the joint probability is close to sum of all joint probabilities, in other words if there are no other plausible state paths, then the point estimate returned by the algorithm will be reliable. Let’s see how it performs for our splice site model. The following code implements the Viterbi algorithm by reading in a previously inferred HMM to analyze a novel sequence:

import csv
import numpy
import sys

neginf = float("-inf")

def read_fasta(fasta_path):
	label = None
	sequence = None

	fasta_sequences = {}

	fasta_file = open(fasta_path)

	l = fasta_file.readline()
	while l != "":
		if l[0] == ">":
			if label != None:
				fasta_sequences[label] = sequence

			label = l[1:].strip()
			sequence = ""
		elif label != None:
			sequence += l.strip()

		l = fasta_file.readline()

	fasta_file.close()

	if label != None:
		fasta_sequences[label] = sequence

	return fasta_sequences

def read_matrix(matrix_path):
	matrix_file = open(matrix_path)
	matrix_reader = csv.reader(matrix_file)

	column_names = next(matrix_reader)

	list_of_numeric_rows = []
	for row in matrix_reader:
		numeric_row = numpy.array([float(x) for x in row])
		list_of_numeric_rows.append(numeric_row)

	matrix_file.close()

	matrix = numpy.stack(list_of_numeric_rows)

	return column_names, matrix

# ignore warnings caused by zero probability states
numpy.seterr(divide = "ignore")

emission_matrix_path     = sys.argv[1]
transmission_matrix_path = sys.argv[2]
fasta_path               = sys.argv[3]

sequence_alphabet, e_matrix = read_matrix(emission_matrix_path)
hidden_state_alphabet, t_matrix = read_matrix(transmission_matrix_path)

log_e_matrix = numpy.log(e_matrix)
log_t_matrix = numpy.log(t_matrix)

m = len(hidden_state_alphabet) # the number of hidden states

fasta_sequences = read_fasta(fasta_path)

for sequence_name in fasta_sequences:
	sequence = fasta_sequences[sequence_name]

	n = len(sequence) # the length of the sequence and index of the last position

	# the first character is also offset by 1, for pseudo-1-based-addressing
	numeric_sequence = numpy.zeros(n + 1, dtype = numpy.uint8)
	for i in range(n):
		numeric_sequence[i + 1] = sequence_alphabet.index(sequence[i])

	# all calculations will be in log space
	v_matrix = numpy.zeros((m, n + 1)) # Viterbi log probabilities
	p_matrix = numpy.zeros((m, n + 1), dtype = numpy.uint8) # Viterbi pointers

	# initialize matrix probabilities
	v_matrix.fill(neginf)
	v_matrix[0, 0] = 0.0

	temp_vitebri_probabilities = numpy.zeros(m)

	for i in range(1, n + 1):
		for k in range(1, m): # state at i
			for j in range(m): # state at i - 1
				e = log_e_matrix[k, numeric_sequence[i]]
				t = log_t_matrix[j, k]
				v = v_matrix[j, i - 1]

				temp_vitebri_probabilities[j] = e + t + v

			v_matrix[k, i] = numpy.max(temp_vitebri_probabilities)
			p_matrix[k, i] = numpy.argmax(temp_vitebri_probabilities)

	# initialize the maximum a posteriori hidden state path using the state with
	# the highest joint probability at the last position
	map_state = numpy.argmax(v_matrix[:, n])

	# then follow the pointers backwards from (n - 1) to 0
	for i in reversed(range(n)):
		subsequent_map_state = map_state
		map_state = p_matrix[subsequent_map_state, i + 1]

		if map_state != subsequent_map_state:
			print("Transition from %s at position %d to %s at position %d" % (hidden_state_alphabet[map_state], i, hidden_state_alphabet[subsequent_map_state], i + 1))

The first and second arguments for this program are paths to the emission matrix and transmission matrix respectively. A simplified version of the emission matrix from the previously inferred gene structure HMM looks like this:

A,C,G,T
0000,0.0000,0.0000,0.0000
2905,0.2018,0.2349,0.2728
0952,0.0327,0.7735,0.0986
0011,0.0000,0.9988,0.0001
2786,0.1581,0.1581,0.4052
0000,0.0010,0.9989,0.0001
2535,0.1039,0.5197,0.1229

And a simplified version of the transition matrix looks like this:

start,exon interior,exon 3',intron 5',intron interior,intron 3',exon 5'
0000,1.0000,0.0000,0.0000,0.0000,0.0000,0.0000
0000,0.9962,0.0038,0.0000,0.0000,0.0000,0.0000
0000,0.0000,0.0000,1.0000,0.0000,0.0000,0.0000
0000,0.0000,0.0000,0.0000,1.0000,0.0000,0.0000
0000,0.0000,0.0000,0.0000,0.9935,0.0065,0.0000
0000,0.0000,0.0000,0.0000,0.0000,0.0000,1.0000
0000,1.0000,0.0000,0.0000,0.0000,0.0000,0.0000

We can analyse the Arabidopsis gene FOLB2 (which codes for an enzyme that is part of the folate biosynthesis pathway). Warning: this is committing the cardinal sin of testing a model using data from the training set, which you should not do in real life! This gene has two introns, one within the 5’ untranslated region (UTR) and the other inside the coding sequence.

The third argument of the program is a path to a FASTA format sequence file, and the sequence of FOLB2 between the UTRs in FASTA format is:

>FOLB2
ATGGAGAAAGACATGGCAATGATGGGAGACAAACTGATACTGAGAGGCTTGAAATTTTATGGTTTCCATGGAGCTATTCC
TGAAGAGAAGACGCTTGGCCAGATGTTTATGCTTGACATCGATGCTTGGATGTGTCTCAAAAAGGCTGGTCTATCAGACA
ACTTAGCTGATTCTGTCAGCTATGTCGACATTTACAAGTTAGTTTTAATTACTAATATGAGAGGATTTGCTAGAGATAGT
TAACTAAATTCTCCCCTTTACTCTTGACCAATCCATTTTTATTGTGACCTCATCCAAAAATGACAAGCTTTGCTTATATA
ACAATTTGTCATCACTATCTGTGTCACTGAGTGATGCATTGATTATAGGATATGAAATGATTCTTTGAGATTGAAGATTT
GAAAAGGTTGTGTGTAGGTTATGTAGTAGTGACTACACTTTTCATATGCTGTGTTTGAAACTGTATCATAATTTGTTTTG
GAATGGAATGAATAATCTTAGCGTGGCAAAGGAAGTTGTAGAAGGGTCATCAAGAAACCTTCTGGAGAGAGTTGCAGGAC
TTATAGCTTCCAAAACTCTGGAAATATCCCCTCGGATAACAGCTGTTCGAGTGAAGCTATGGAAGCCAAATGTTGCGCTT
ATTCAAAGCACTATCGATTATTTAGGTGTCGAGATTTTCAGAGATCGCGCAACTGAATAA

Save the matrices and sequences to their own files, then run the Viterbi code with the paths to those files as the arguments. The Viterbi algorithm does detect an intron, but it gets the splice site positions wrong. This failure demonstrates the core problem of the algorithm on its own; it gives us an answer but without any sense of its probability. For that, we need the forward and backward algorithms.

For another perspective on the Viterbi algorithm, consult lesson 10.6 of Bioinformatics Algorithms by Compeau and Pevzner.

Optimal in the sense of finding the true maximum a posteriori (MAP) solution, not in the sense of finding the true path. ↩
MCMC run for an infinite number of steps should also be exact (conditional on the Markov chain being ergodic). In practice, because we do not have infinite time to conduct scientific research, MCMC is not guaranteed to sample exactly proportionally to the target distribution. ↩

COMP571 (Fall 2020, a.k.a. COVID times)

2020-08-03T09:00:00-05:00

Who

Instructor:

Huw A. Ogilvie
hao3@rice.edu

TAs:

Zhi Yan
zy20@rice.edu

Where and when

This year, in-person attendance will be entirely optional. Your choice to take COMP571 online should make as little difference to your experience or results as possible. You can change your mind during the semester and stop or start in-person attendance. The situation is dynamic and in-person attendance may or may not be possible for the entire semester, but online attendance will always remain an option.

Distribution of class materials and submission of assignments and projects will be conducted via Canvas.

Lectures will be held in Duncan Hall 1046, on Tuesdays and Thursdays, between 3:10–4:30 PM. If you want to attend lectures in-person, you will have to nominate whether you want to attend on Tuesday or Thursdays. To ensure reduced class sizes for social distancing, you should not attend both days in-person. All lectures will be recorded and uploaded after they are delivered. Lectures will not be streamed live.

One scheduled office hour will be held every Friday at 10am on Zoom, and attendance by the whole class is encouraged so that everyone can benefit from the discussion. Office hours will not be recorded. Individual appointments outside this time are welcome.

Intended audience

Course objectives and learning outcomes

Course materials

The main material for this course will be lectures and the course blog. The text for Professor Treangen’s course Genome-Scale Algorithms is Bioinformatics Algorithms by Compeau & Pevzner, which contains relevant chapters and is now available for free online. However the focus of COMP571 is on the nexus of sequence analysis and statistical models, whereas the focus of Bioinformatics Algorithms and Professor Treangen’s course is on algorithms and data structures.

Software for the course

Then simply use the Python package manage pip to install NumPy and SciPy from the command line, by running pip3 install numpy scipy.

Schedule and assessment

The course is organized around three themes, and there will be a corresponding homework assignment for each one;

Models and algorithms used for sequence alignment
Hidden Markov Models in computational biology
Phylogenetic and coalescent inference

Project design and discussion will take place either on Zoom or in socially distanced outdoor environments depending on the preference and physical location of students in each group.

The below schedule may change subject to Rice University policy

Monday’s date	Tuesday’s lecture	Thursday’s lecture	Homework	Project
08/24/20	Introduction	Canceled due to hurricane
08/31/20	Central dogma and motifs ¹	PSSMs¹
09/07/20	Pseudocounts and Dirichlet¹	BLOSUM and PAM¹
09/14/20	Global alignment¹	Local alignment and BLAST¹	#1 issued
09/21/20	E-values and affine gap scheme¹	Cancelled
09/28/20	(Hidden) Markov Models²	(Hidden) Markov Models²	#1 due
10/05/20	Viterbi algorithm²	Forward algorithm²
10/12/20	Backward algorithm²	Phylogenetic trees³	#2 issued
10/19/20	Equal-cost parsimony³	Unequal-cost parsimony³		#1 due
10/26/20			#2 due
11/02/20	Hill climbing³	SPR and initialization
11/09/20	The Felsenstein zone³	Felsenstein’s pruning algorithm³
11/16/20	GTR models³	Coalescent theory³	#3 issued	#2 due
11/23/20	No instruction	No instruction
11/30/20	No instruction	No instruction	#3 due
12/07/20	No instruction	No instruction		#3 due

Each row in the above table lists the lecture topics, homework and project milestones for the week beginning on the specified Monday and ending the following Sunday. Superscript numbers refer to the theme(s) for that day’s class or midterm. Assignments will be issued before midnight on the Sunday at the end of the week. Assignments and projects will also be due before midnight on Sundays at the end of the week.

Grade policies

Homework assignments: 20% each
Project design: 10%
Project implementation: 10%
Project report: 20%

No assignments or projects will be accepted after the end of the semester on Wednesday, December 16, 2020. In exceptional circumstances, if a student is unable to complete an assignment or project before the semester ends, the final percentage will be calculated by scaling the assessment which that student has completed. Again, this will be solely within the instructor’s purview.

Absence policies

Please stay safe and healthy. Do your best to either attend or view lectures and participate in project meetings.

Rice Honor Code

Students with a disability

Calculating the likelihood for an ultrametric tree (example)

2019-12-04T08:00:00-06:00

In this example we will calculate the likelihood $P(D|T,h)$ where $D$ is a single site, $T$ is a rooted tree topology, and $h$ is the node heights for the tree topology. Since we are using node heights instead of branch lengths, and if we make the node heights at the tips all zeros, the tree is necessarily ultrametric. The site pattern, topology and branch lengths correspond to the following tree:

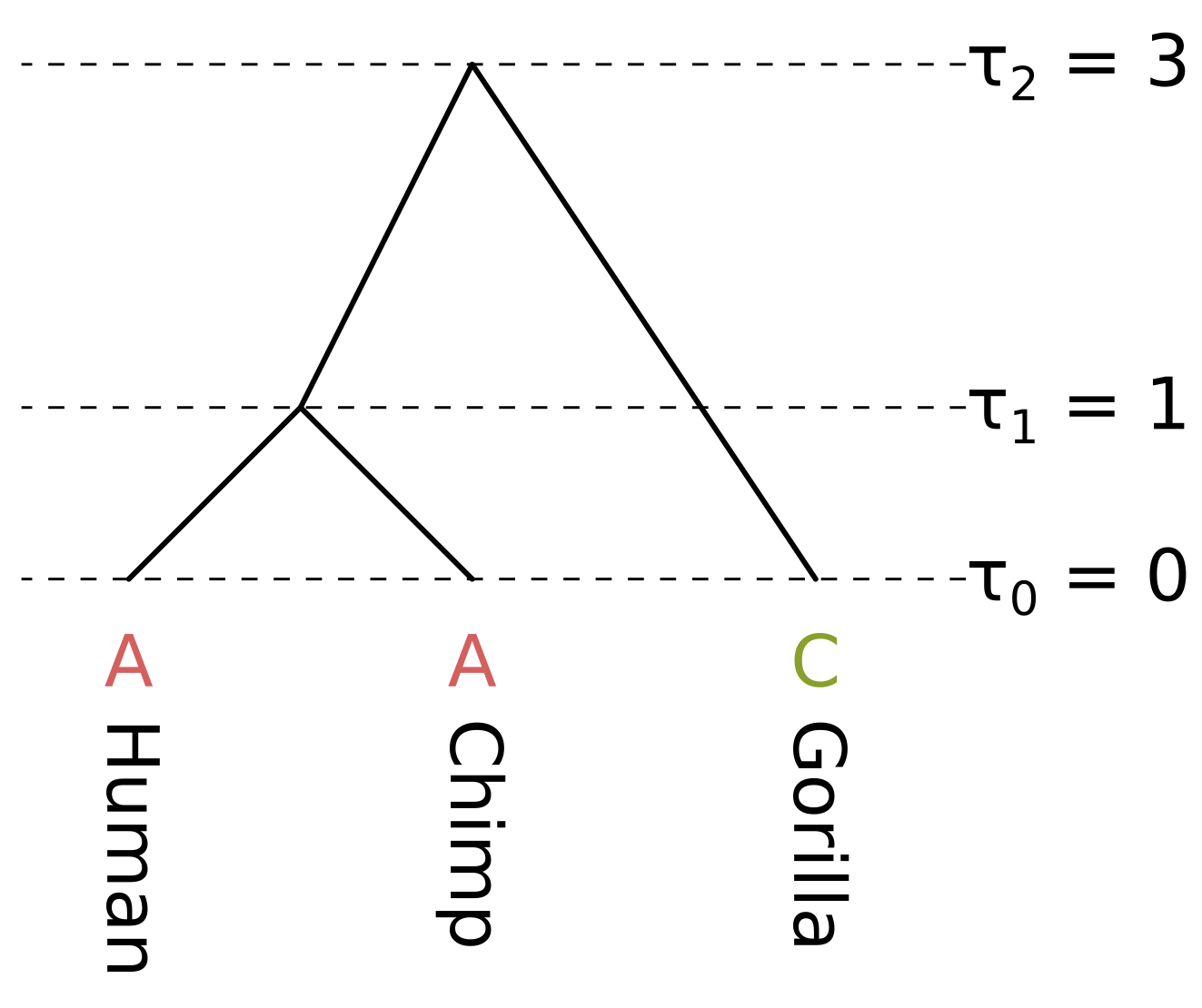
The node heights $\tau$ are given in some unit of time $t$ before present. As long as the substitution rate $\mu$ is constant across the tree (i.e. we are assuming a strict molecular clock), there are three unique branch lengths $l = \mu t$ in expected substitutions per site. In this example we assume a constant rate $\mu = 0.1$.

The branch lengths of humans and chimps in substitutions per site are both 0.1, the branch length of the ancestor of humans and chimps (HC) is 0.2, and the branch length of gorillas is 0.3. We will calculate the likelihood under the Jukes–Cantor model, so we only have to calculate the probability of the state being the same by the end of a branch (e.g. A to A), and the probability of the state being something else (e.g. A to C), given the state at the beginning and the branch length.

For the human and chimp branches, these will be (to four decimal places):

\[P_{xx}(0.1) = \frac{1}{4}\left(1 + 3e^{-\frac{4}{3}0.1}\right) = 0.9064\] \[P_{xy}(0.1) = \frac{1}{4}\left(1 - e^{-\frac{4}{3}0.1}\right) = 0.0312\]

For the HC branch, these will be:

\[P_{xx}(0.2) = \frac{1}{4}\left(1 + 3e^{-\frac{4}{3}0.2}\right) = 0.8245\] \[P_{xy}(0.2) = \frac{1}{4}\left(1 - e^{-\frac{4}{3}0.2}\right) = 0.0585\]

For the gorilla branch, these will be:

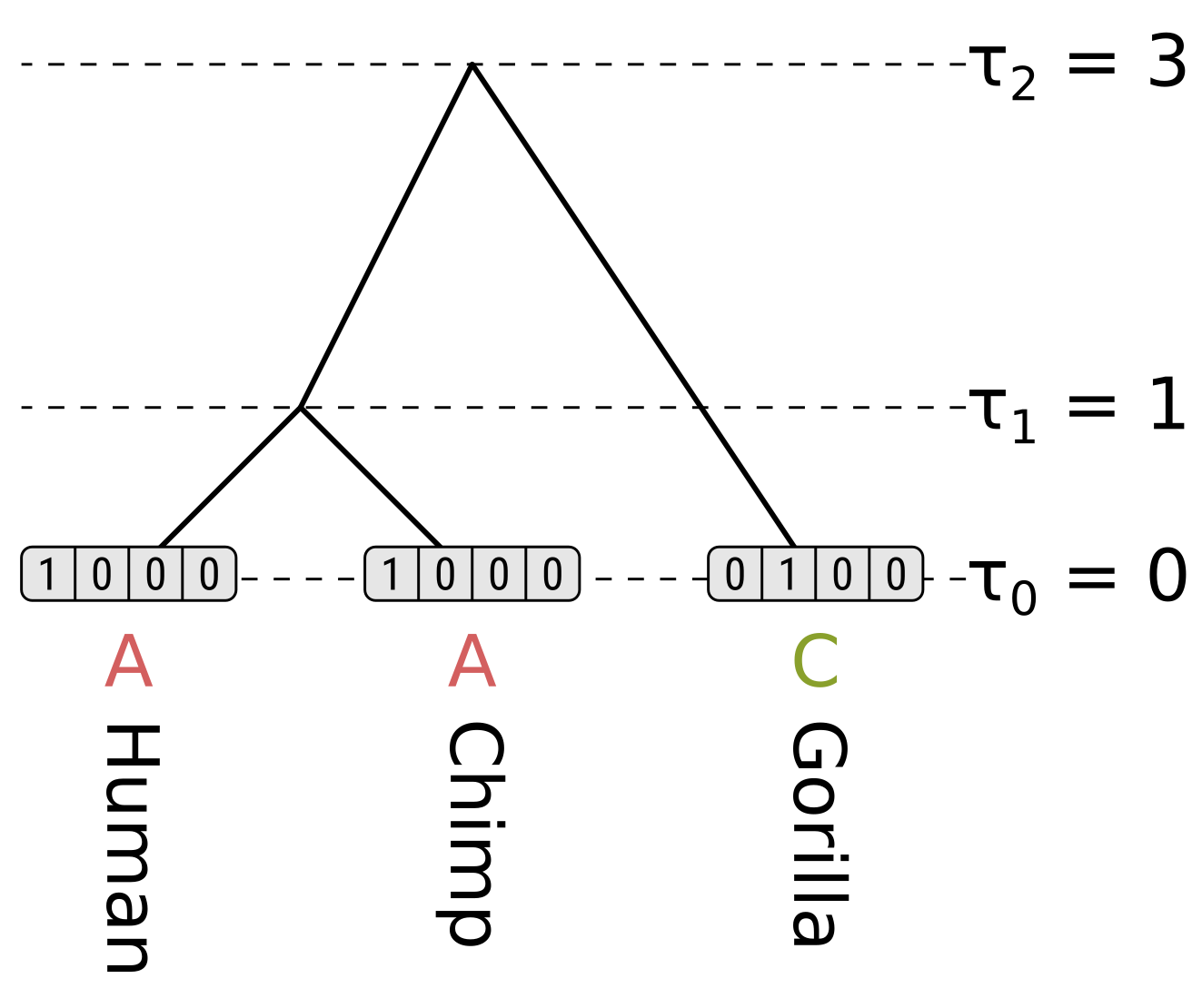
\[P_{xx}(0.3) = \frac{1}{4}\left(1 + 3e^{-\frac{4}{3}0.3}\right) = 0.7528\] \[P_{xy}(0.3) = \frac{1}{4}\left(1 - e^{-\frac{4}{3}0.3}\right) = 0.0824\]

For the tip nodes, the partial likelihoods are 1 for the observed states, and 0 otherwise:

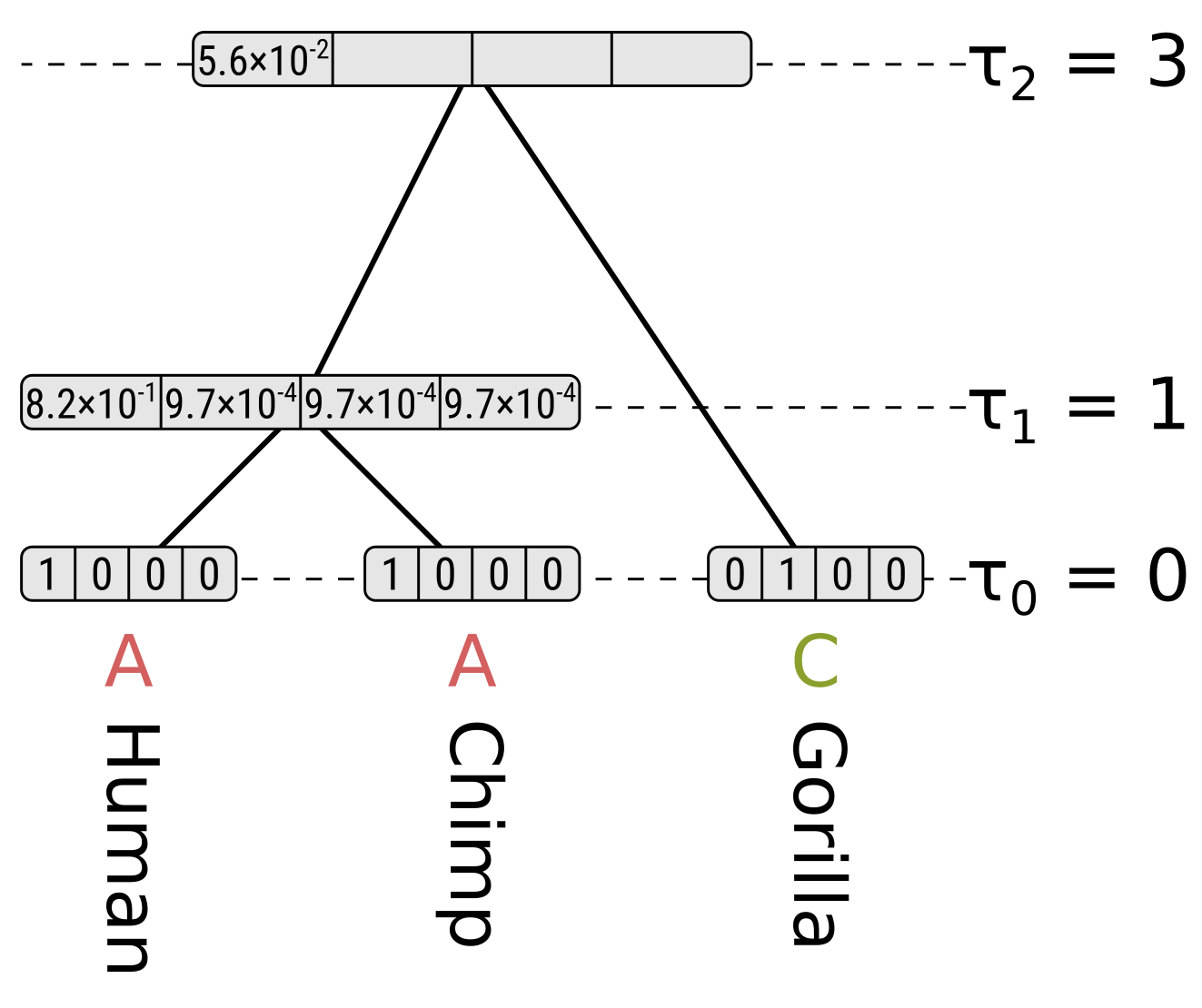
For each internal node we have to consider the left and right children separately. We will start off by calculating the partial likelihood of state A of the HC internal node. Beginning with the left child (humans), the probability of the child state being A is the probability of the end state being the same (as calculated above), multiplied by the partial likelihood of the child state. This is $0.9064 \times 1 = 0.9064$. For child states C, G and T, the probabilities will be $0.0312 \times 0 = 0$, so the probability for the left child branch integrating over all child states is $0.9064 + 0 + 0 + 0 = 0.9064$.

The right child (chimpanzees) has the same branch length and partial likelihoods, so its probability will also be $0.9064$, and the partial likelihood of state A for the HC node will be $0.9064 \times 0.9064 = 0.8215$. We use the product because we want to calculate the probability of the left and right subtree states.

For state C in the HC node, the probability along the left branch for child state A will be $0.0312 \times 1 = 0.0312$. The probability for state C will be $0.9064 \times 0 = 0$, and for states G and T will be $0.0312 \times 0 = 0$. So the probability for the left branch integrating over child states will be $0.0312$. Again the right branch will be the same, so the partial likelihood of state C will be $0.0312 \times 0.0312 = 0.00097$

Because of the equal base frequencies and equal rates assumption in Jukes–Cantor, the partial likelihoods of G and T will be the same as for C.

Now for state A at the root, the probability along the left branch for child state A will be the probability of the state remaining the same given a branch length of 0.2, multiplied by the partial likelihood of state A for the HC node, or $0.8245 \times 0.8215 = 0.6773$. For child states C, G and T it will be $0.0585 \times 0.00097 = 0.000057$, which is the probability of the state being different at the end given a branch length of 0.2 multiplied by the partial likelihoods. So the probability along the left branch for state A at the root integrating over the left child states will be $0.6773 + 3 \times 0.000057 = 0.6775$.

For the right child (gorillas) only state C has a non-zero partial likelihood, so we should multiply the above by the probability of a different state given the branch length 0.3 to get the partial likelihood of state A at the root, which will be $0.6775 \times 0.0824 = 0.0558$.

For state C at the root, the probability of child state A along the left (HC) branch will be $0.0585 \times 0.8215 = 0.0481$, the probability of child state C will be $0.8245 \times 0.00097 = 0.0008$, and the probabilities of child states G or T will be $0.0585 \times 0.00097 = 0.000057$. So integrating over the child states for the left branch, the probability will be $0.0481 + 0.0008 + 2 \times 0.000057 = 0.0490$. Again because of the symmetry in Jukes–Cantor, the probability along the left branch will be the same for root states G and T.

However for state C at the root, the probability along the right (gorilla) branch will be the probability of the same state at the end given a branch length of 0.3, but for states G and T the probabilities will be for a different state. So for state C at the root the partial likelihood will be $0.0490 \times 0.7528 = 0.0369$, but for states G and T their partial likelihoods will be $0.0490 \times 0.0824 = 0.0040$.

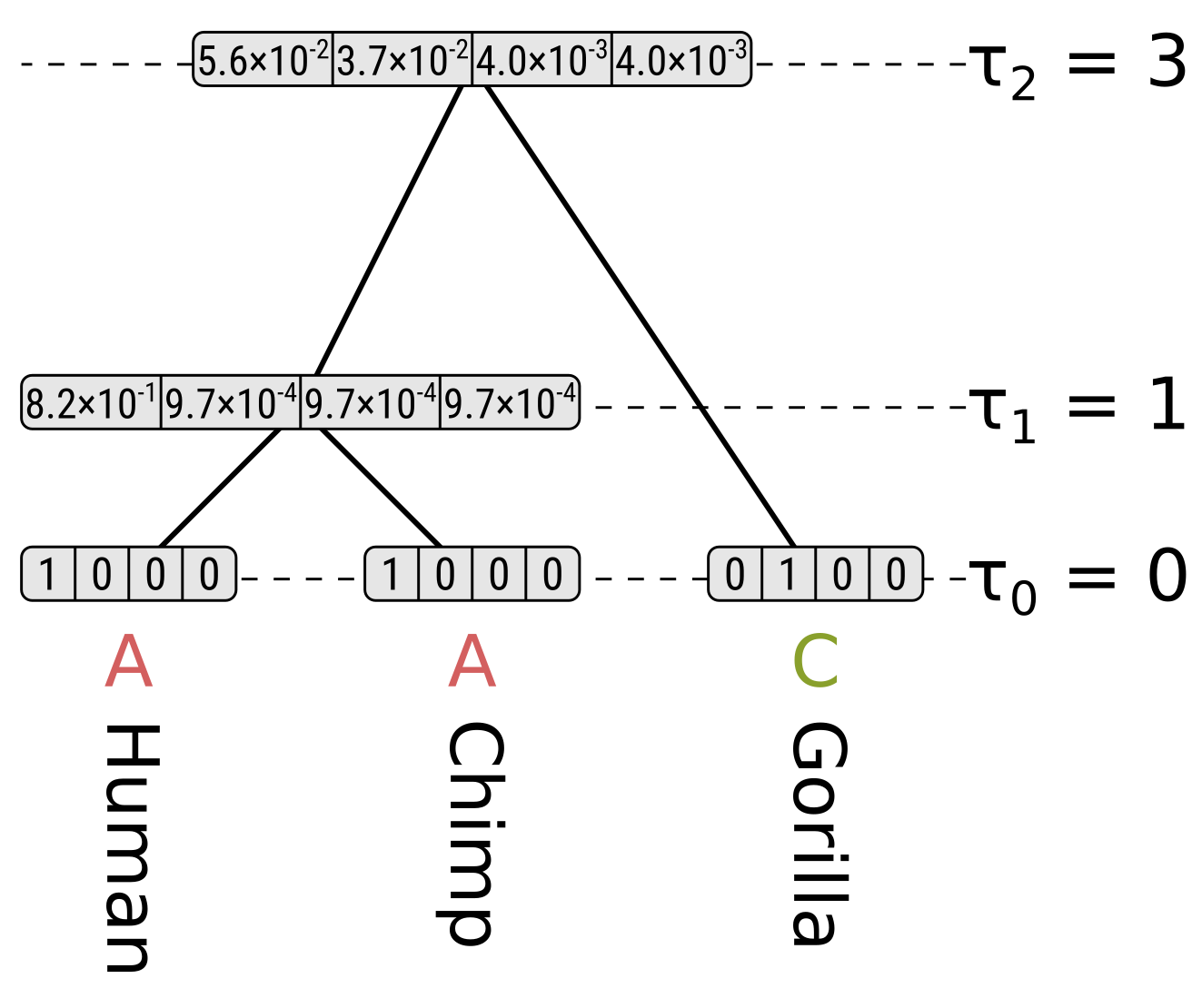
Each partial likelihood for a node $n$ is conditioned on the state $k$ at that node $P(D|n=k,T,h)$, but to calculate the likelihood at a node $P(D|T,h)$ we need to integrate over the probabilities $P(D,n=k|T,h)$ for each state at that node. Following the chain rule, we can convert the conditional likelihoods to joint probabilities by multipling the partials by the base (stationary) frequencies. For Jukes–Cantor the base frequencies are all equal and hence $\frac{1}{4}$ given there are 4 nucleotide states.

So we can calculate the likelihood for the entire tree by summing the root partial likelihoods and dividing by 4. For this tree and site, the likelihood $P(D|T,h) = \frac{0.0588 + 0.0369 + 2 \times 0.0040}{4} = 0.0252$.

Hill climbing and NNI

2019-12-02T08:00:00-06:00

The Sankoff algorithm can efficiently calculate the parsimony score of a tree topology. Felsenstein’s pruning algorithm can efficiently calculate the probability of a multiple sequence alignment given a tree with branch lengths and a substitution model. But how can the tree with the lowest parsimony score, or highest likelihood, or highest posterior probability be identified?

Possibly the simplest algorithm that can do this for most kinds of inference is hill-climbing. This algorithm basically works like this for maximum likelihood inference:

Initialize the parameters $\theta$
Calculate the likelihood $L = P(D\vert\theta)$
Propose a small modification to $\theta$ and call it $\theta'$
Calculate the likelihood $L' = P(D\vert\theta')$
If $L' > L$, accept $\theta \leftarrow \theta'$ and $L \leftarrow L'$
If stopping criteria are not met, go to 3

You may notice that without stopping criteria, the algorithm is an infinite loop. How do we know when to give up? Three obvious criteria that can be used are:

Stop after a certain number of proposals are rejected in a row (without being interrupted by any successful proposals)
Stop after running the algorithm for a certain length of time
Stop after running the algorithm for a certain number of iterations through the loop

For maximum a posteriori inference, we also need to calculate the prior probability $P(\theta)$. Because the marginal likelihood $P(D)$ does not change, following Bayes’ rule the posterior probability $P(\theta\vert D)$ is proportional to $P(D\vert\theta)P(\theta)$, which we might call the unnormalized posterior probability. So instead of maximizing the likelihood, we instead maximize the product of the likelihood and prior, which we have to recalculate for each proposal. The algorithm becomes:

Initialize the parameters $\theta$
Calculate the unnormalized posterior probability $P = P(D\vert\theta)P(\theta)$
Propose a small modification to $\theta$ and call it $\theta'$
Calculate the unnormalized posterior probability $P' = P(D\vert\theta')P(\theta')$
If $P' > P$, accept $\theta \leftarrow \theta'$ and $P \leftarrow P'$
If stopping criteria are not met, go to 3

For maximum parsimony inference, we simply need to calculate the parsimony score of our parameters, so I will describe this as a function $f(D,\theta)$ which returns the parsimony score. The algorithm becomes:

Initialize the parameters $\theta$
Calculate the parsimony score $S = f(D,\theta)$
Propose a small modification to $\theta$ and call it $\theta'$
Calculate the parsimony score $S' = f(D,\theta')$
If $S' < S$, accept $\theta \leftarrow \theta'$ and $S \leftarrow S'$
If stopping criteria are not met, go to 3

Note that the inequality is reversed in step 5 for maximum parsimony. These are all described for general cases, but for phylogenetic inference $\theta$ will correspond to a tree topology, and possibly branch lengths (for non-ultrametric trees) or node heights (for ultrametric trees). Maximum parsimony is unaffected by branch lengths, so $\theta$ is only the tree topology. Proposing changes to branch lengths or node heights is relatively simple because we can use some kind of uniform, Gaussian or other proposal distribution. But how do we propose a small change to the tree topology?

A huge amount of research has gone into tree changing “operators,” but the simplest and most straightforward is nearest-neighbor interchange, or NNI. This works by isolating an internal branch of a tree, which for an unrooted tree always has four connected branches. The four nodes at the end of the connected branches may be tips or other internal nodes, because NNI can work on trees of any size.

One of the nodes is fixed in place (in this example, humans), and its sister node is exchanged with one of the two other nodes.

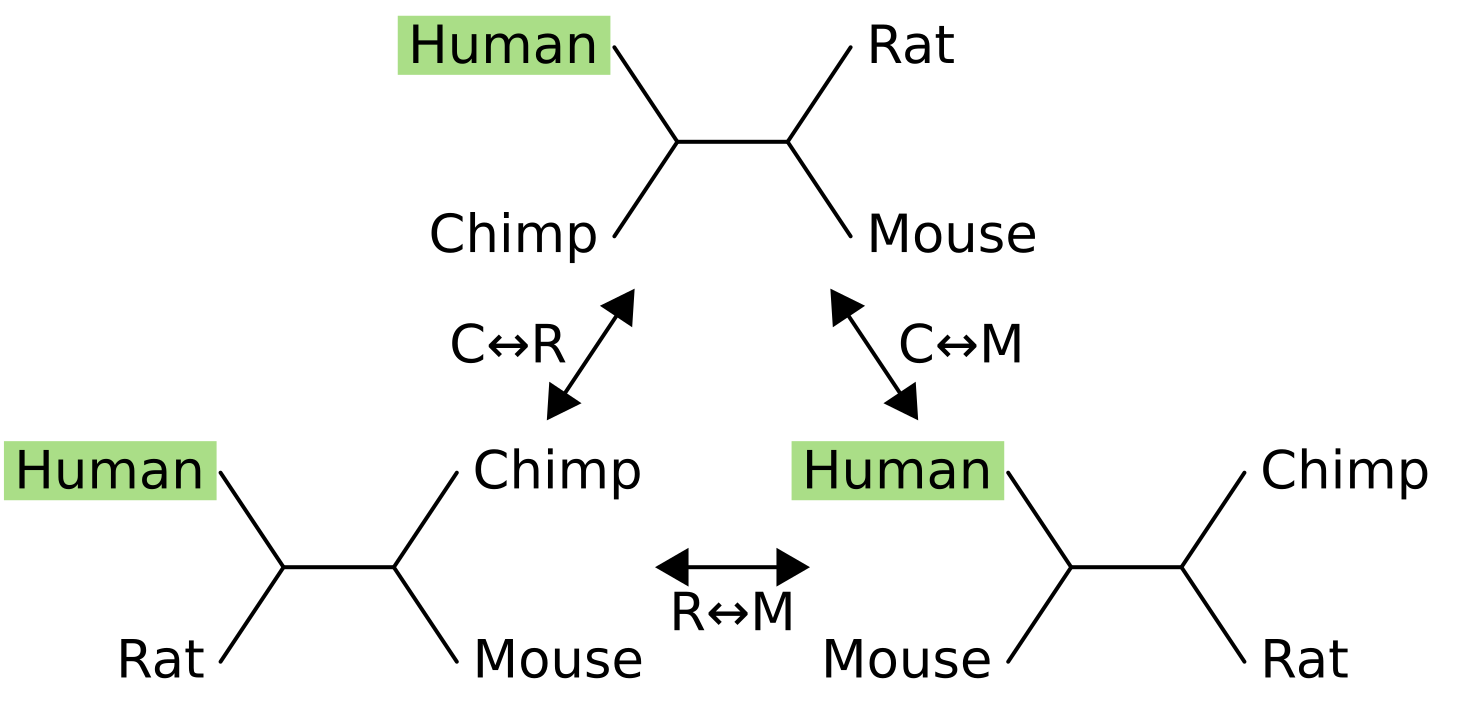
For example the NNI move from the tree at the top to the tree in the bottom-right exchanges mouse (M) with chimpanzee (C), causing the sister of humans to change from chimps to mice. For four taxon trees there are only three topologies, and they are all connected by a single NNI move. For five taxon unrooted trees there are fifteen topologies and not all are connected:

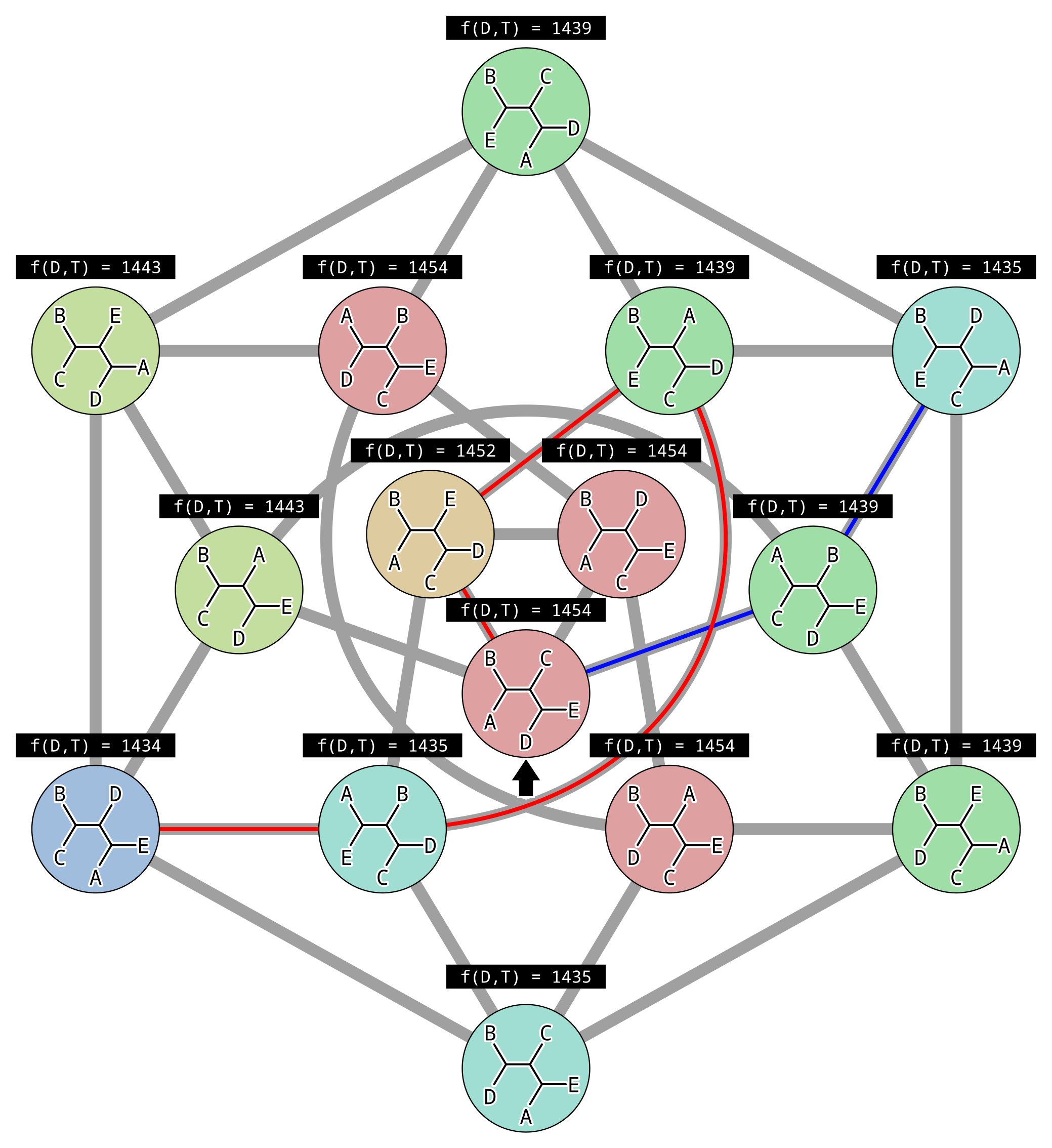
In the above example, each gray line represents an NNI move between topologies, and there is (made-up) parsimony scores above each topology. There are two peaks in parsimony score, one for the tree (((A,E),D),(B,C)) where the parsimony score is 1434, and one for the tree (((B,E),D),(A,C)) where the parsimony score is 1435. Since the second peak has a higher parsimony score, it is a local and not the global optimal solution.

This illustrates the biggest problem with hill climbing. Because we only accept changes that improve the score, once we reach a peak where all connected points in parameter space (unrooted topologies in this case) are worse, then we can never climb down. Imagine we initialized our hill climbing using the topology indicated by the black arrow. By chance we could have followed the red path to the globally optimal solution… or the blue path to a local optimum.

One straightforward way to address this weak point is to run hill climbing multiple times. The likelihood, unnormalized posterior probability or parsimony scores of the final accepted states for each hill climb can be compared, and the best solution out of all runs accepted, in the hope that it corresponds to the global optimum.

What about NNI for rooted trees? It works in a very similar way, but we have to pretend that there is an “origin” tip above the root node, and perform the operation on the unrooted equivalent of the rooted tree.

As with unrooted NNI, we can now pick any internal branch of the tree to rotate subtrees or taxa around. Connected to the head of an internal branch of a rooted tree is two child branches, and connected to the tail is a parent branch and “sister” branch. For rooted NNI, we fix the parent branch and swap its sister with one of the child branches.

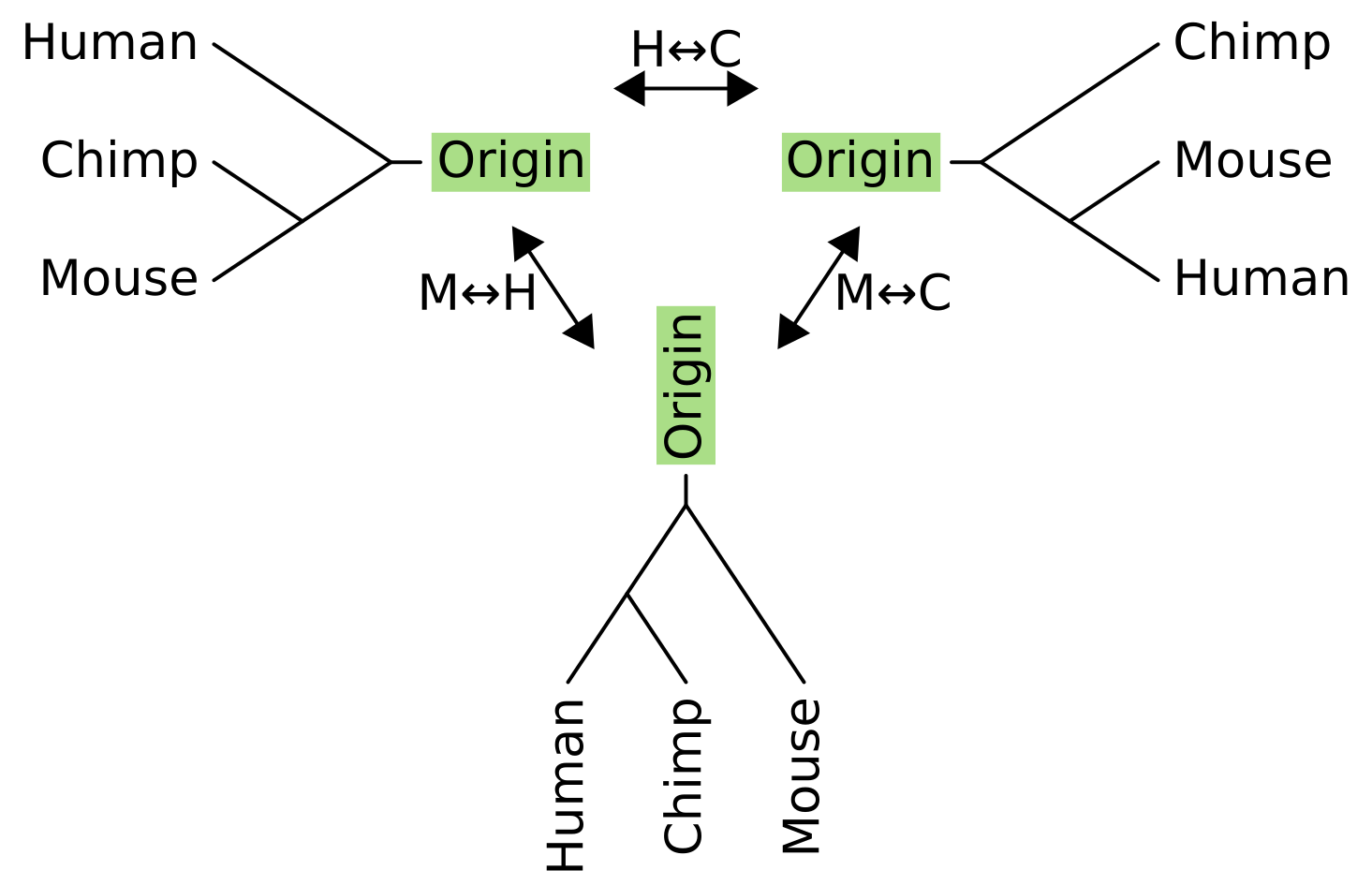
For three taxon rooted trees, there is only one internal branch and the parent of this internal branch is the origin. In this example, the sister to the origin for the tree on the left is humans, so the NNI operations exchange humans with either chimps (becoming the tree on the right), or with mice (becoming the tree on the bottom).

And how do we initialize hill climbing in phylogenetics? There are a few ways.

Randomly generate a tree using simulation
Permute the taxon labels on a predefined tree
Use neighbor-joining if the tree is unrooted
Use UPGMA if the tree is rooted

The first method implies a particular model is being used to generate the tree. Models from the birth-death family or from the coalescent family are often used for this task. Another possibility is to use a beta-splitting model, see Sainudiin & Véber (2016).

The latter two methods have the advantage of starting closer to the optimal solutions, reducing the time required for a single hill climb. However when running hill climbing multiple times, the first two methods have the advantage of making the different runs more independent of each other, and therefore more likely for one to find the global optimum.

Long branch attraction (in the Felsenstein zone)

2019-12-01T08:00:00-06:00

Long branch attraction is the phenomenon where two branches which are in truth not sisters are inferred to be sister branches when using maximum parsimony inference. This occurs because, unlike likelihood, parsimony does not take into account branch lengths when computing the parsimony score.

Maximum likelihood inference considers all sites when calculating the likelihood, but only so-called “parsimony informative sites” will end up determining the tree inferred using maximum parsimony. These are sites where at least two tips share a state, and at least two other tips share a state which is different from the first state.

Consider the case of humans, chimps, rats and mice. In truth, humans and chimps should be sisters, as should rats and mice. The parsimony informative sites that support the true tree topology will therefore be those where humans and chimps share a state, and rats and mice share a state which is different from the human/chimp state (site patterns on the left in the below figure).

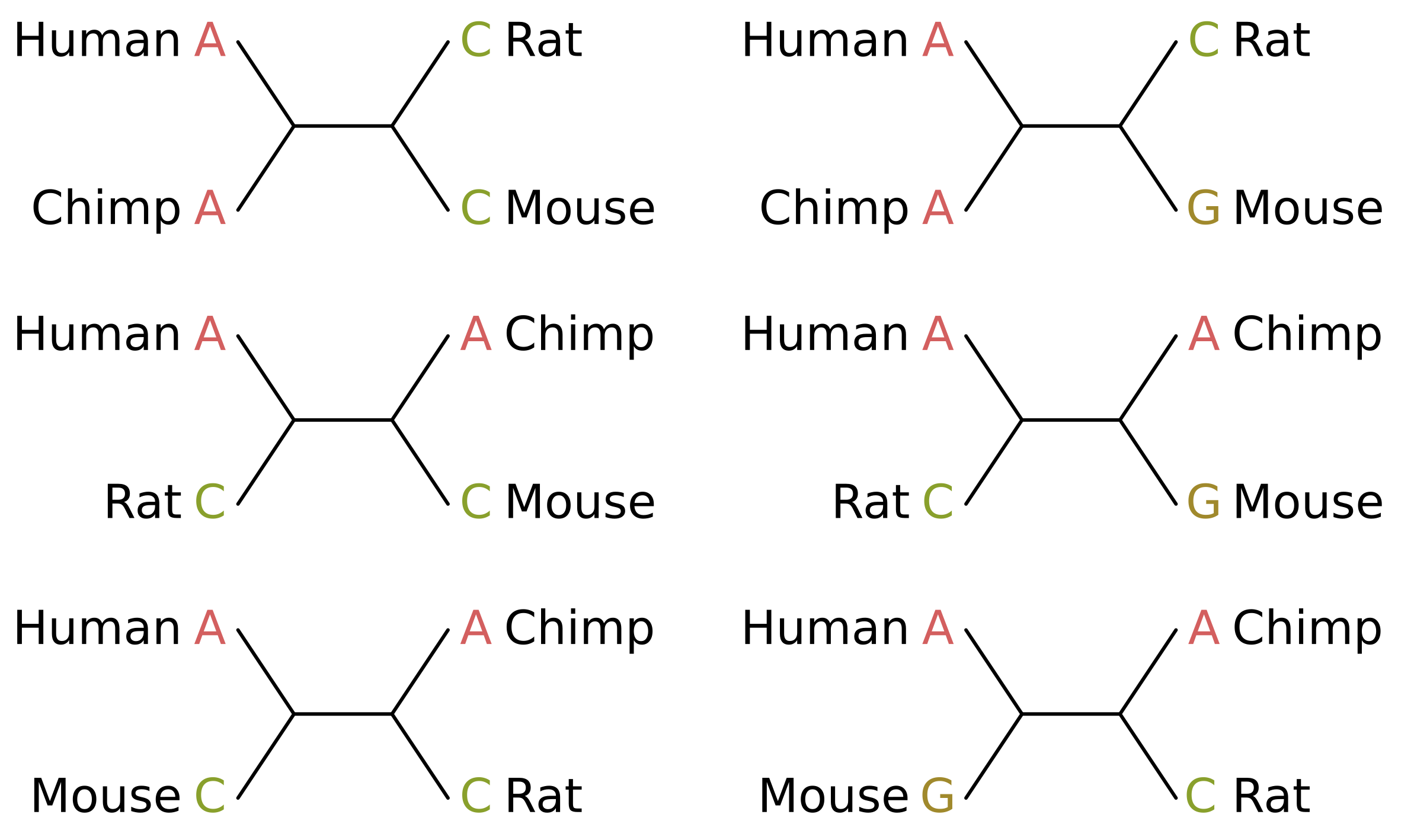
The score of those sites given the true topology (top-left in the above figure) will be 1 for equal-cost parsimony. Given one of the two incorrect unrooted topologies (middle-left and bottom-left), the score of those sites will be 2, because at least two mutations along the tree are required to explain the site pattern.

For the uninformative sites, e.g. if we give mice a different state from every other species (site patterns on the right), at least two mutations will be required for all topologies and the score will always be 2 (see trees on the right). The contribution of these sites is therefore a constant and does not affect the inference.

So if the number of parsimony informative site patterns supporting one of the incorrect topologies is greater than the number of informative site patterns supporting the true topology, the best scoring topology will be incorrect and our inferred topology will be wrong.

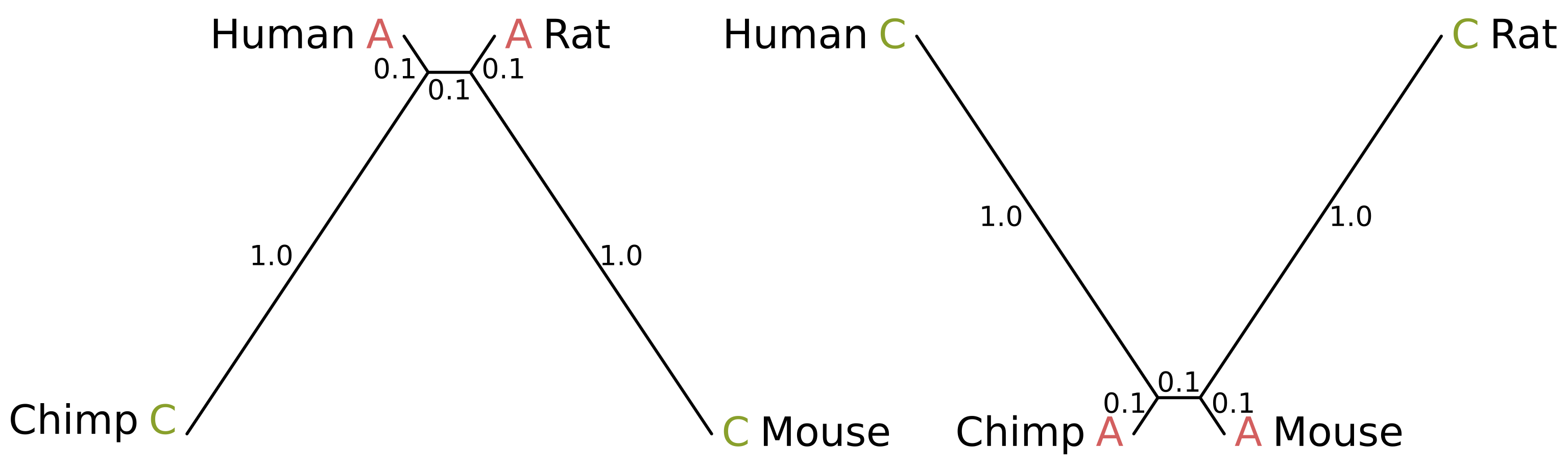
Felsenstein zone trees with branch lengths in substitutions per site

How can this be possible? Consider the above-right tree. Because the internal branch is short, and the chimp and mouse branches are also short, the probability of mutation along those three branches is minimal. Chimps and mice are therefore likely to share a state. But because the human and rat branches are long, the probability of mutation is high.

Given a lack of mutation elsewhere, if a mutation or mutations in the human and rat branches cause the human and rat states to differ, the site will be uninformative. But if convergent mutations occur, the resulting site will be parsimony informative and support the incorrect topology where humans and rats are sister species (for example, the above site patterns).

These sites will contribute a score of 2 to the true topology and a score of 1 to the human-rat topology when using equal-cost parsimony, the inverse of the contribution from parsimony informative sites that support the true human-chimp topology. So if more of the human-rat supporting sites are in a data set than human-chimp supporting sites, the wrong topology will be inferred using maximum parsimony.

How likely is this to occur? I simulated sequence alignments for a range of branch lengths, beginning with the above-left branch lengths, gradually increasing the human and rat lengths (l1) while decreasing the chimp and mouse lengths (l2), ending with the above-right branch lengths. The internal branch length was always 0.1 substitutions per site. Jukes-Cantor was used as the substitution model, 1 million sites were simulated per alignment. For each set of branch lengths I counted the percentage of parsimony informative sites supporting the correct topology and the percentage supporting the human-rat or human-mouse topologies.

You can see that when l1 is greater than somewhere between 0.75 and 0.8 or less than somewhere between 0.3 and 0.35, the number of parsimony informative sites supporting the human-rat topology becomes greater than the number supporting the human-rat topology. These crossovers mark the border of the Felsenstein zone.

For both Dollo and equal rates models of evolution, whether a four-taxon tree is in the Felsenstein zone can be tested analytically rather than by simulation. For details, see Felsenstein’s paper, “Cases in which parsimony or compatibility methods will be positively misleading,” published in Systematic Zoology (now known as Systematic Biology) in 1978.

Likelihood of a tree

2019-11-27T08:00:00-06:00

The likelihood of a tree is the probability of a multiple sequence alignment or matrix of trait states (commonly known as a character matrix) given a tree topology, branch lengths and substitution model. An efficient dynamic programming algorithm to compute this probability was first developed by Felsenstein in 1973, and is quite similar to the algorithm used to infer unequal-cost parsimony scores developed by Sankoff in 1975.

As with the Sankoff algorithm, a vector is associated with each node of the tree. Each element of the vector stores the probability of observing the tip states, given the tree below the associated node and the state corresponding to the element (the first, second, third and fourth elements usually correspond to A, C, G and T for DNA).

Those probabilities marginalize over all possible states at every internal node below the root of the subtree. These are known as partial likelihoods, and are in contrast with the vector elements of the Sankoff algorithm, which are calculated only from the states which minimize the total cost. We might write the partial likelihood for state $k$ at node $n$ as:

\[P_{n,k} = P(D_i|k, T, l, M)\]

where $D_i$ is the tip states at position $i$ of the multiple sequence alignment or character matrix, $T$ is the topology of the subtree under the node, $l$ is the branch lengths of the subtree, and $M$ is the substitution model. I will go over the five key differences between the two algorithms.

One. For the Sankoff algorithm the elements in the vectors at the tips are initialized to either zero for the observed states or infinity otherwise, because the only the observed state can be the state at the tips. However because partial likelihoods are probabilities not costs, for likelihood they are initialized to 1 for 100% probability (or 0 if working in log space) for the observed states, and 0 for 0% probability (or negative infinity if working in log space).

Two. Because Felsenstein’s likelihood depends on branch lengths and not just topology, the transition probabilities must be recomputed for each branch. For the Jukes-Cantor model just two probabilties are needed because it assumes equal base frequencies and transition rates. The first is the probability of state $k$ at the parent node and state $k'$ at the child node being the same conditioned on the $k$:

\[P(k' = k|k) = P_{xx} = \frac{1}{4}(1 + 3 e^{-\frac{4}{3}\mu t})\]

where $\mu t$ is the product of the substitution rate and length of the branch in time, which is the length of the branch in substitutions per site. And the second is the probability of the state at the child node being different, again conditioned on the state at the parent node:

\[P(k' \ne k|k) = P_{xy} = \frac{1}{4}(1 - e^{-\frac{4}{3}\mu t})\]

Three. Because the partial likelihoods marginalize over the internal node states, for each child branch the probabilities for all child node states must be summed over rather than finding the minimum cost. Using Jukes-Cantor, when calculating the partial likelihood for state $k$ at node $n$, for the one case where the state $k'$ at the child node $c$ equals $k$, the probability is $P_{xx} P_{c,k'}$. For the three cases where it does not, the probabilities are $P_{xy}P_{c,k'}$. By summing all four probabilities, we marginalize over the possible states at that child node.

Four. Cost accumulates, but the joint probability of independent variables multiplies. So for parsimony the cost of the left and right subtrees under a node (stored in the vectors associated with the left and right children) and the cost of the mutations along the left and right child branches (if any) are all added together. But for likelihood the left and right marginal probabilities are multiplied. Why are left and right marginal probabilities independent? Because sequences evolve independently along left and right subtrees, conditioned on the state at the root.

This also applies when calculating the cost or likelihood of a sequence alignment or character matrix. For maximum parsimony the cost accumulates for each additional site, so the parsimony score of an alignment is the sum of minimum costs for each site. But for maximum likelihood the likelihood of each site is a probability and we treat each site as evolving independently, so the likelihood for the alignment is the product of site likelihoods.

Five. For maximum parsimony, the smallest element of the root node vector gives the parsimony score of the tree. But for Felsenstein’s likelihood, we want to marginalize over root states, i.e. we want $P(D_i|T,l,M)$ which does not depend on state $k$ at the root. Given the RNA alphabet $\{A,C,G,U\}$, we can perform this marginalization by summing over the joint probabilities:

But the partial likelihoods at the root give us $P(D_i|k, T, l, M)$, where state $k$ is on the right side of the conditional. We can use the chain rule to convert them to joint probabilities:

\[P(D_i,k|T,l,M) = P(D_i|k,T,l,M) \cdot P(k)\]

but what is $P(k)$? It is the stationary frequency of the state, which for Jukes-Cantor is always $\frac{1}{4}$, so for that substitution model we just have to sum the partial likelihoods at the root and divide by four to get the likelihood of the tree.

The following code will calculate the likelihood of a tree (in Newick format) for a multiple sequence alignment (MSA in FASTA format), with the paths to the tree and MSA files given as the first and second arguments to the program.

import ete3
import numpy
import os.path
import sys

neginf = float("-inf")

# used by read_fasta to turn a sequence string into a vector of integers based
# on the supplied alphabet
def vectorize_sequence(sequence, alphabet):
	sequence_length = len(sequence)

	sequence_vector = numpy.zeros(sequence_length, dtype = numpy.uint8)

	for i, char in enumerate(sequence):
		sequence_vector[i] = alphabet.index(char)

	return sequence_vector

# this is a function that reads in a multiple sequence alignment stored in
# FASTA format, and turns it into a matrix
def read_fasta(fasta_path, alphabet):
	label_order = []
	sequence_matrix = numpy.zeros(0, dtype = numpy.uint8)

	fasta_file = open(fasta_path)

	l = fasta_file.readline()
	while l != "":
		l_strip = l.rstrip() # strip out newline characters

		if l[0] == ">":
			label = l_strip[1:]
			label_order.append(label)
		else:
			sequence_vector = vectorize_sequence(l_strip, alphabet)
			sequence_matrix = numpy.concatenate((sequence_matrix, sequence_vector))

		l = fasta_file.readline()

	fasta_file.close()

	n_sequences = len(label_order)
	sequence_length = len(sequence_matrix) // n_sequences
	sequence_matrix = sequence_matrix.reshape(n_sequences, sequence_length)

	return label_order, sequence_matrix

# this is a function that reads in a phylogenetic tree stored in newick
# format, and turns it into an ete3 tree object
def read_newick(newick_path):
	newick_file = open(newick_path)
	newick = newick_file.read().strip()
	newick_file.close()

	tree = ete3.Tree(newick)

	return tree

def recurse_likelihood(node, site_i, n_states):
	if node.is_leaf():
		node.partial_likelihoods.fill(0) # reset the leaf likelihoods
		leaf_state = node.sequence[site_i]
		node.partial_likelihoods[leaf_state] = 1
	else:
		left_child, right_child = node.get_children()

		recurse_likelihood(left_child, site_i, n_states)
		recurse_likelihood(right_child, site_i, n_states)

		for node_state in range(n_states):
			left_partial_likelihood = 0.0
			right_partial_likelihood = 0.0
			for child_state in range(n_states):
				if node_state == child_state:
					left_partial_likelihood += left_child.pxx * left_child.partial_likelihoods[child_state]
					right_partial_likelihood += right_child.pxx * right_child.partial_likelihoods[child_state]
				else:
					left_partial_likelihood += left_child.pxy * left_child.partial_likelihoods[child_state]
					right_partial_likelihood += right_child.pxy * right_child.partial_likelihoods[child_state]

			node.partial_likelihoods[node_state] = left_partial_likelihood * right_partial_likelihood

# nucleotides, obviously
alphabet = "ACGT" # A = 0, C = 1, G = 2, T = 3
n_states = len(alphabet)

# this script requires a newick tree file and fasta sequence file, and
# the paths to those two files are given as arguments to this script

tree_path = sys.argv[1]
root_node = read_newick(tree_path)

msa_path = sys.argv[2]
taxa, alignment = read_fasta(msa_path, alphabet)
site_count = len(alignment[0])

# the number of taxa, and the number of nodes in a rooted phylogeny with that
# number of taxa
n_taxa = len(taxa)
n_nodes = n_taxa + n_taxa - 1

for node in root_node.traverse():
	# initialize a vector of partial likelihoods that we can reuse for each site
	node.partial_likelihoods = numpy.zeros(n_states)

	# we can precalculate the pxx and pxy values for the branch associated with
	# this node
	node.pxx = (1 / 4) * (1 + 3 * numpy.exp(-(4 / 3) * node.dist))
	node.pxy = (1 / 4) * (1 - numpy.exp(-(4 / 3) * node.dist))

	# add sequences to leaves
	if node.is_leaf():
		taxon = node.name
		taxon_i = taxa.index(taxon)
		node.sequence = alignment[taxon_i]

# this will be the total likelihood of all sites
log_likelihood = 0.0

for site_i in range(site_count):
	recurse_likelihood(root_node, site_i, n_states)

	# need to multiply the partial likelihoods by the stationary frequencies
	# which for Jukes-Cantor is 1/4 for all states
	log_likelihood += numpy.log(numpy.sum(root_node.partial_likelihoods * (1 / 4)))

tree_filename = os.path.split(tree_path)[1]
msa_filename = os.path.split(msa_path)[1]

tree_name = os.path.splitext(tree_filename)[0]
msa_name = os.path.splitext(msa_filename)[0]

print("The log likelihood P(%s|%s) = %f" % (msa_name, tree_name, log_likelihood))