Contact Info Publications Papers Talks			Selected Papers Image Deformation Using Moving Least Squares Schaefer S., McPhail T. and Warren J. To appear in ACM SIGGRAPH 2006 Abstract: We provide an image deformation method based on Moving Least Squares using various classes of linear functions including affine, similarity and rigid transformations. These deformations are realistic and give the user the impression of manipulating real-world objects. We also allow the user to specify the deformations using either sets of points or line segments, the later useful for controlling curves and profiles present in the image. For each of these techniques, we provide simple closed-form solutions that yield fast deformations, which can be performed in real-time. A Unified, Integral Construction For Coordinates Over Closed Curves Schaefer S., Ju T. and Warren J. To appear in Computer-Aided Geometric Design 2006 Abstract: We propose a simple generalization of Shephard's interpolation to piecewise smooth, convex closed curves that yields a family of boundary interpolants with linear precision. Two instances of this family reduce to previously known interpolants: one based on a generalization of Wachspress coordinates to smooth curves and the other an integral version of mean value coordinates for smooth curves. A third instance of this family yields a previously unknown generalization of discrete harmonic coordinates to smooth curves. For closed, piecewise linear curves, we prove that our interpolant reproduces a general family of barycentric coordinates considered by Floater, Hormann and Kos that includes Wachspress coordinates, mean value coordinates and discrete harmonic coordinates. 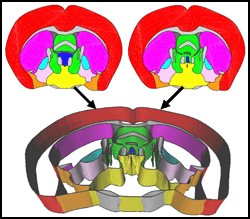Building 3D surface networks from 2D curve networks with application to anatomical modeling T. Ju, J. Warren, J. Carson, G. Eichele, C. Thaller, W. Chiu, M. Bello and I. Kakadiaris Proceedings of Pacific Graphics, to appear, 2005 We present a novel method that automatically constructs a surface network from curve networks with arbitrary topology and partitioning an arbitrary number of materials. The surface network exactly interpolates the curve network on each plane and is guaranteed to be free of gaps or self-intersections. In addition, our method provides a flexible framework for user interaction so that the surface topology can be modified conveniently when necessary. As an application, we applied the method to build a high-resolution 3D model of the mouse brain from 2D anatomical boundaries defined on 350 tissue sections. 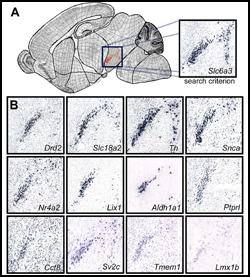A Digital Atlas to Characterize the Mouse Brain Transcriptome J. Carson, T. Ju, H. Lu, C. Thaller, M. Xu, S. Pallas, M. C. Crair, J. Warren, W. Chiu and G. Eichele PLoS Computational Biology, to appear, 2005 Here we have developed a computational method for annotating gene expression patterns in the context of a digital atlas to facilitate custom user-queries and comparisons of this type of data. This procedure has been applied to 200 genes in the postnatal mouse brain. As an illustration of utility, we identify candidate genes that may be related to Parkinson's disease by using the expression of a dopamine transporter in the substantia nigra as a search query pattern. In addition, we discover that transcription factor Rorb is down-regulated in the barrelless mutant relative to control mice by quantitative comparison of expression patterns in layer IV somatosensory cortex. 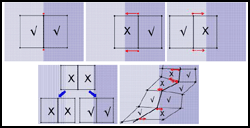Hybrid Segmentation Framework for Tissue Images Containing Gene Expression Data M. Bello, T. Ju, J. Warren, J. Carson, W. Chiu, C. Thaller, G. Eichele and I. Kakadiaris Proceedings of MICCAI, to appear, 2005 In this work, we propose a new automatic method that results in the segmentation of gene expression images into distinct anatomical regions in which the expression can be quantified and compared with other images. Our method utilizes models of shape of training images, texture differentiation at region boundaries, and features of anatomical landmarks to deform a subdivision mesh-based atlas to fit gene expression images. 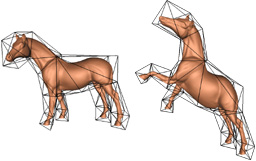Mean Value Coordinates for Closed Triangular Meshes Ju T., Schaefer S. and Warren J. ACM SIGGRAPH 2005, pages 561-566 Abstract: Constructing a function that interpolates a set of values defined at vertices of a mesh is a fundamental operation in computer graphics. Such an interpolant has many uses in applications such as shading, parameterization and deformation. For closed polygons, mean value coordinates have been proven to be an excellent method for constructing such an interpolant. In this paper, we generalize mean value coordinates from closed 2D polygons to closed triangular meshes. Given such a mesh P, we show that these coordinates are continuous everywhere and smooth on the interior of P. The coordinates are linear on the triangles of P and can reproduce linear functions on the interior of P. To illustrate their usefulness, we conclude by considering several interesting applications including constructing volumetric textures and surface deformation. A Geometric Construction of Coordinates for Convex Polyhedra using Polar Duals Ju T., Schaefer S., Warren J., Desbrun M. Eurographics Symposium on Geometry Processing 2005, pages 181-186 Abstract: A fundamental problem in geometry processing is that of expressing a point inside a convex polyhedron as a combination of the vertices of the polyhedron. Instances of this problem arise often in mesh parameterization and 3D deformation. A related problem is to express a vector lying in a convex cone as a non-negative combination of edge rays of this cone. This problem also arises in many applications such as planar graph embedding and spherical parameterization. In this paper, we present a unified geometric construction for building these weighted combinations using the notion of polar duals. We show that our method yields a simple geometric construction for Wachspress's barycentric coordinates, as well as for constructing Colin de Verdiere matrices from convex polyhedra---a critical step in Lovasz's method with applications to parameterizations. Dual Marching Cubes: Primal Contouring of Dual Grids Schaefer S. and Warren J. Proceedings of Pacific Graphics 2004, pages 70-76 Abstract: We present a method for contouring an implicit function using a grid topologically dual to structured grids such as octrees. By aligning the vertices of the dual grid with the features of the implicit function, we are able to reproduce thin features without excessive subdivision required by methods such as Marching Cubes or Dual Contouring. Dual Marching Cubes produces a crack-free, adaptive polygonalization of the surface that reproduces sharp features. Our approach maintains the advantage of using structured grids for operations such as CSG while being able to conform to the relevant features of the implicit function yielding much sparser polygonalizations than has been possible using structured grids. 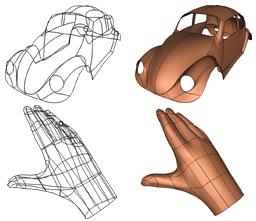Lofting Curve Networks using Subdivision Surfaces Schaefer S., Warren J. and Zorin D. Eurographics Symposium on Graphics Processing 2004, pages 105-116. Abstract: Lofting is a traditional technique for creating a curved shape by first specifying a network of curves that approximates the desired shape and then interpolating these curves with a smooth surface. This paper addresses the problem of lofting from the viewpoint of subdivision. In particular, we develop two new subdivision schemes; a univariate scheme that converges to a network of cubic splines and a modified Catmull-Clark scheme that lofts these curve networks. Near the curve network, these lofted subdivision surfaces are C^2 except for those points where three or more curves meet at which the surface is C^1 with bounded curvature. As a demonstration of these two methods, we have constructed an automatic system that quadrangulates these curve networks using a novel method and fairs the surfaces produced by our subdivision scheme. Smooth Subdivision of Tetrahedral Meshes Schaefer S., Hakenberg J. and Warren J. Eurographics Symposium on Graphics Processing 2004, pages 151-158. Abstract: We describe a new subdivision scheme for unstructured tetrahedral meshes. Previous tetrahderal schemes based on generalizations of box splines have encoded arbitrary directional preferences in their associated subdivision rules that were not reflected in tetrahderal base mesh. Our method avoids this choice of preferred directions resulting a scheme that is simple to implement via repeated smoothing. In an extended appendix, we analyze this tetrahedral scheme and prove that the scheme generates C^2 deformations everywhere except along edges of the tetrahedral base mesh. Along edges shared by four or more tetrahedra in the base mesh, we present strong evidence that the scheme generates C^1 deformations. 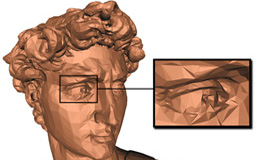Adaptive Vertex Clustering Using Octrees Schaefer S. and Warren J. Proceedings of SIAM Geometric Design and Computing 2003, pages 491-500. Abstract: We present an adaptive vertex clustering approach to out-of-core simplification of polygonal meshes using a dynamic octree. Similar to uniform clustering, our technique utilizes quadratic error functions to position the mesh vertices; however, this new method can resolve vertices to arbitrary resolutions, which allows reproduction of extremely small details and more accurate simplifications. By sorting the vertices of the input mesh, our algorithm dynamically discovers portions of the mesh that are locally complete, which are then available for collapse when the octree grows too large. This adaptive octree is then used to cluster the vertices of the input to generate a simplified mesh. Finally, we show that our method generates the same tree that would be constructed with unbounded memory if our method is given a small amount of space in addition to the size of the output tree. 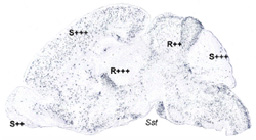Automated Characterization of Gene Expression Patterns with an Atlas of the Mouse Brain Carson J., Ju T., Thaller C., Warren J., Bello M., Kakadiaris I., Chiu W. and Eichele G. To appear in EMBS (2004). A spatio-temporal map of gene activity in the brain would be an important contribution to the understanding of brain development, disease, and function. Such a resource is now possible using high-throughput in situ hybridization, a method for transcriptome-wide acquisition of cellular resolution gene expression patterns in serial tissue sections. However, querying an enormous quantity of image data requires computational methods for describing and organizing gene expression patterns in a consistent manner. In addressing this, we have developed procedures for automated annotation of gene expression patterns in the postnatal mouse brain. Landmark-driven, Atlas-based Segmentation of Mouse Brain Tissue Images Containing Gene Expression Data Kakadiaris I., Bello M., Arunachalam S., Kang W., Ju T., Warren J., Carson J., Chiu W., Thaller C. and Eichele G. To appear in MICCAI (2004). Associating specific gene activity with specific functional locations in the brain anatomy results in a greater understanding of the role of the gene's products. To perform such an association for a large amount of data, reliable automated methods that characterize the distribution of gene expression in relation to a standard anatomical model are required. In this paper, we present an anatomical landmark detection method that has been incorporated into an atlasbased segmentation. The addition of this technique significantly increases the accuracy of automated atlas-deformation. The resulting large-scale annotation will help scientists interpret gene expression patterns more rapidly and accurately. 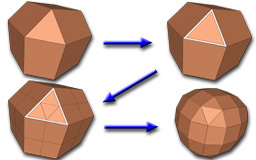On C^2 Triangle/Quad Subdivision Schaefer S. and Warren J. ACM Transactions on Graphics, Vol 24, No. 1 (2005), pages 28-36. This paper describes a subdivision scheme for triangle/quad surfaces that is C^2 everywhere except at extraordinary points where the surface is C^1. The subdivision rules we describe are the same as Stam/Loop's triangle/quad paper except that we apply a preprocessing "unzippering" pass to the mesh, which increases the smoothness on triangle/quad edges from C^1 to C^2. The scheme is practical in that it can be applied to arbitrary meshes including non-manifold meshes. 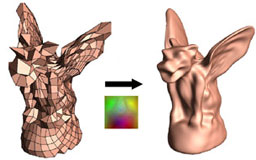Smooth Geometry Images Losasso F., Hoppe H., Schaefer S. and Warren J. Eurographics Symposium on Geometric Processing (2003), pages 138-145. This paper generalizes Hoppe's previous work on geometry images to the smooth case. The paper includes an elegant example of this method used to provide continuous level of detail. 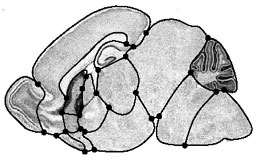A Geometric Database for Gene Expression Data Ju T., Warren J., Eichele G., Thaller C., Chiu W. and Carson J. Eurographics Symposium on Geometric Processing (2003), pages 166-176. This paper describes an application of subdivision meshes to the problem of building a deformable atlas for the mouse brain. In particular, we show that subdivision meshes are ideally suited for building a database that supports queries comparing gene expression data. 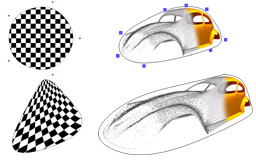Barycentric Coordinates for Convex Sets Warren J., Schaefer S., Hirani A. and Desbrun M. To appear in Advances in Computational and Applied Mathematics This paper superceeds a technical report that we wrote on barycentric coordinates. In particular, we extend the discrete coordinates from Warren 1996 to the continuous case of a convex region bounded by a smooth manifold in arbitrary dimensions. We provide a proof of linear precision for these coordinate functions and describe their application to boundary value problems and freeform deformation. 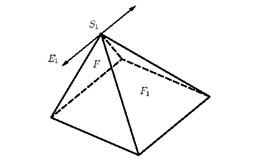On the Uniqueness of Barycentric Coordinates Warren J. Contemporary Mathematics, Proceedings of AGGM02 (2003). Given a convex polytope with m facets in d dimensions, this paper proves there is exactly one set of rational barycentric coordinates for this polytope of degree m-d. These coordinates are exactly the coordinates described in Warren 1996. 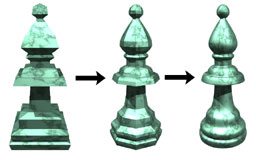A Factored Approach to Subdivision Surfaces Schaefer S. and Warren J. Computer Graphics & Applications, Vol. 24, No. 3 (2004), pages 74-81 This paper is an invited tutorial on the basic of subdivision. Read this paper if you want a non-mathematical introduction to subdivision. Teaching Computer Game Design and Construction Schaefer S. and Warren J. Submitted to a special issue of Computer-Aided Design (2003) This paper describes the author's experience in teaching a senior-level computer gaming class here at Rice University. The paper is written as a how-to manual for others that wish to design and teach such a class. Convex Contouring of Volumetric Data Ju T., Schaefer S. and Warren J. The Visual Computer, Vol. 19, No. 7-8, (2003), pages 513-525 This paper desribes a variant of Marching Cubes that generates contours whose negative space is convex inside each cube. This property is then exploited to build an extremely fast collision detection method. 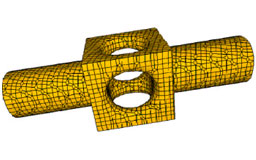Dual Contouring: "The Secret Sauce" Schaefer S. and Warren J. Rice University Technical Report This tech report gives a more detailed description of our implementation of dual contouring. The key technique is a description of how to manipulate and minimize QEFs. 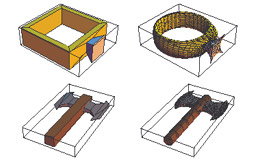Dual Contouring of Hermite Data Ju T., Losasso F., Schaefer S. and Warren J. ACM Transactions on Graphics, Vol. 21, (2002), pages 339-346. This paper introduces a new contouring method that combines a dual method such as SurfaceNets with the sharp feature reproduction of Extended Marching Cubes. The paper includes an elegant algorithm for adaptive contouring. A smooth subdivision scheme for hexahedral meshes Bajaj C., Schaefer S., Warren J. and Xu G. The Visual Computer, Vol. 18, 2002, pages 409-420. This paper describes a trivariate subdivision scheme for hexahedral meshes. The scheme consists of linear subdivision followed by an averaging phase. The scheme converges to a C^2 volume meshes almost everywhere except along extraordinary edges where the scheme is provably C^1 and at extraordinary vertices where the authors supply strong experimental evidence that the scheme is still smooth. 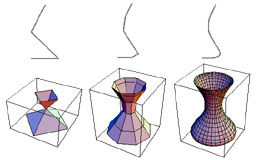A subdivision scheme for surfaces of revolution Morin G., Warren J. and Weimer H. Computer-Aided Geometric Design, Vol. 18, 2001, pages 483-502. This paper describes a simple generalization of the Catmull-Clark subdivision scheme that is capable of exactly reproducing surfaces of revolution. 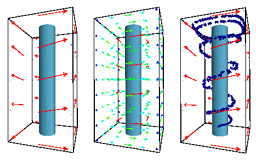Subdivision schemes for fluid flow Weimer H. and Warren J. SIGGRAPH 99 conference proceedings, pages 111-120. This paper describes a vector subdivision scheme that, given a coarse vector field, converges to continuous vector that approximates the original coarse vector field and approximately satisfies the partial diffirential equations for various types of linear flow. 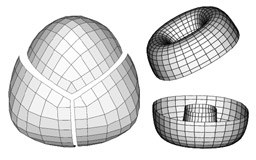Edge and vertex insertion for a class of C^1 subdivision surfaces Habib A. and Warren J. Computer-Aided Geometric Design, 16 (1999), pages 223-247. This paper describes a generalization of the C^1 four direction quadratic box-spline to arbitrary topologies. Additional rules are given that allow "sharp" features to be inserted into these splines in a manner analogous to that of quadratic B-splines. 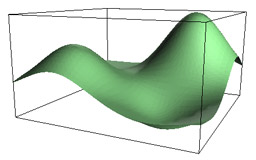Subdivision schemes for thin plate splines Weimer H. and Warren J. Proceedings of Eurographics, Computer Graphics Forum, Vol. 17, No. 3, 1998, pages 303-313 & 392. This paper derives a subdivision scheme that converges to locally supported approximations to thin plate splines. 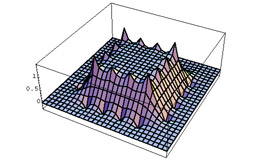Subdivision schemes for variational splines Weimer H. and Warren J. Approximation theory IX (1998), pages 345-352. This paper illustrates the relation between variational problem and subdivision schemes. Specifically, the solution space to a wide range of variational problems can be captured as a spline space defined through subdivision. Multi-resolution analysis for surfaces of arbitrary topological type Lounsbery M., DeRose T. and Warren J. ACM Transactions on Graphics, Vol. 16, No. 1, 1997, pages 34-73. This paper describes a general method for doing multi-resolution analysis over irregular geometry. The key building block is to define scaling functions over irregular geometry via subdivision. 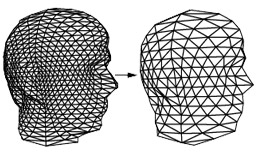Sparse filter banks for binary subdivision schemes Warren J. Mathematics of surface VII (1996). This paper describes a simple, local method for building sparse synthesis and analysis filters given a sequence of binary subdivision matrices. These filters banks can used as the building blocks for multi-resolution analysis. Barycentric coordinates for convex polytopes Warren J. Advances in Computational Mathematics, Vol. 6, No. 2, 1996, pages 97-108. This paper gives a general construction for a special type of coordinate system over a convex polytope. This barycentric coordinate system has a set of coordinate functions, one per vertex, that are nonnegative over the polytope, sum to one, and reproduce linear functions. An Efficient Evaluation Algorithm for Polynomials in the Polya Basis Warren J. Computing, Vol. 24, 1995, pages 1-5. This paper discuss an extension of Newton's method for evaluating polynomials in the monomial basis to the more general Polya basis. Binary subdivision scheme for functions over irregular knot sequences Warren J. Mathematical Methods in CAGD III, (1995) This paper describes and analyzes univariate subdivision schemes over irregular spacings. Multi-sided rational surfaces patches with independent boundary control Warren J. Design and Application of Curves and Surfaces: Mathematics of Surfaces V (1994), pages 281-294. This paper analyzes several schemes for building surface patches with more that four sides. The common theme shared by these schemes is the rational coordinates functions must have singularities at well-defined locations. 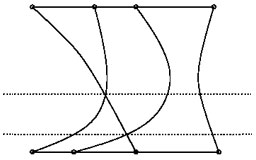Factoring Rational Polynomials over the Complex Numbers Bajaj C., Canny J., Garrity T. and Warren J. SIAM Journal of Computing, Vol. 22, No. 2, 1993. This paper describes a clever method for factoring polynomials using geometric techniques. 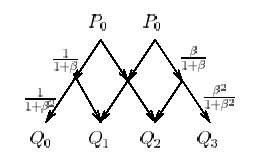An Extension of Chaiken's Algorithm to B-Spline Curves with Knots in Geometric Progression Goldman R. and Warren J. Computer Graphics, Vision, and Information Processing, Vol. 55, No. 1, 1993, pages 58-61. This paper discusses a simple clever modification of Chaikin's algorithm to allow subdivision of B-spline whose knots lie in geometric progression. 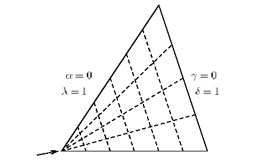Creating Multi-Sided Rational Bezier Surfaces using Base Points Warren J. ACM Transactions on Graphics, Vol. 11, No. 2, 1992, pages 127-139. This paper describes a technique for creating extra sides on a rational Bezier patch by setting the weights of corner control points to zero. This technique can be used to understand the behavior of Gregory patches. 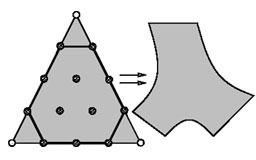A Bound on the Implicit Degree of Polygonal Bezier Surfaces Warren J. Algebraic Geometry and Applications (1991). This paper gives a simple constructive proof of the implicit degree of multi-sided rational Bezier patches with a given Newton polygon. Subdivision methods for geometric design Warren J. A monograph on subdivision written in 1994 that formed an initial draft for the subsequent book Subdivision Methods For Geometric Design: A Constructive Approach, published by Morgan Kaufmann in 2002. Selected Talks Analysis Techniques for Subdivision Surfaces Invited talk at the Symposium on Geometry Processing 2004