Equal-cost parsimony

The principle behind maximum parsimony based inference is to explain the data using the smallest cost. In its most basic form, all events are given equal cost, so a nucleotide changing from A to C (a transversion) is given the same cost as a change from C to T (a transition). Likewise the gain of a trait, e.g. flight, is given the same cost as the loss of that trait. In this case finding the explanation with the smallest cost is the same as finding the explanation with the smallest number of events. In a phylogenetic context, the explanation is the tree topology, and the events are mutations of molecular sequences or organismal traits.

Equal cost parsimony can be solved using a simple procedure called the Fitch algorithm (Fitch, 1971). The output of this algorithm is the smallest number of events required to explain the pattern of one site or trait for a given tree topology.

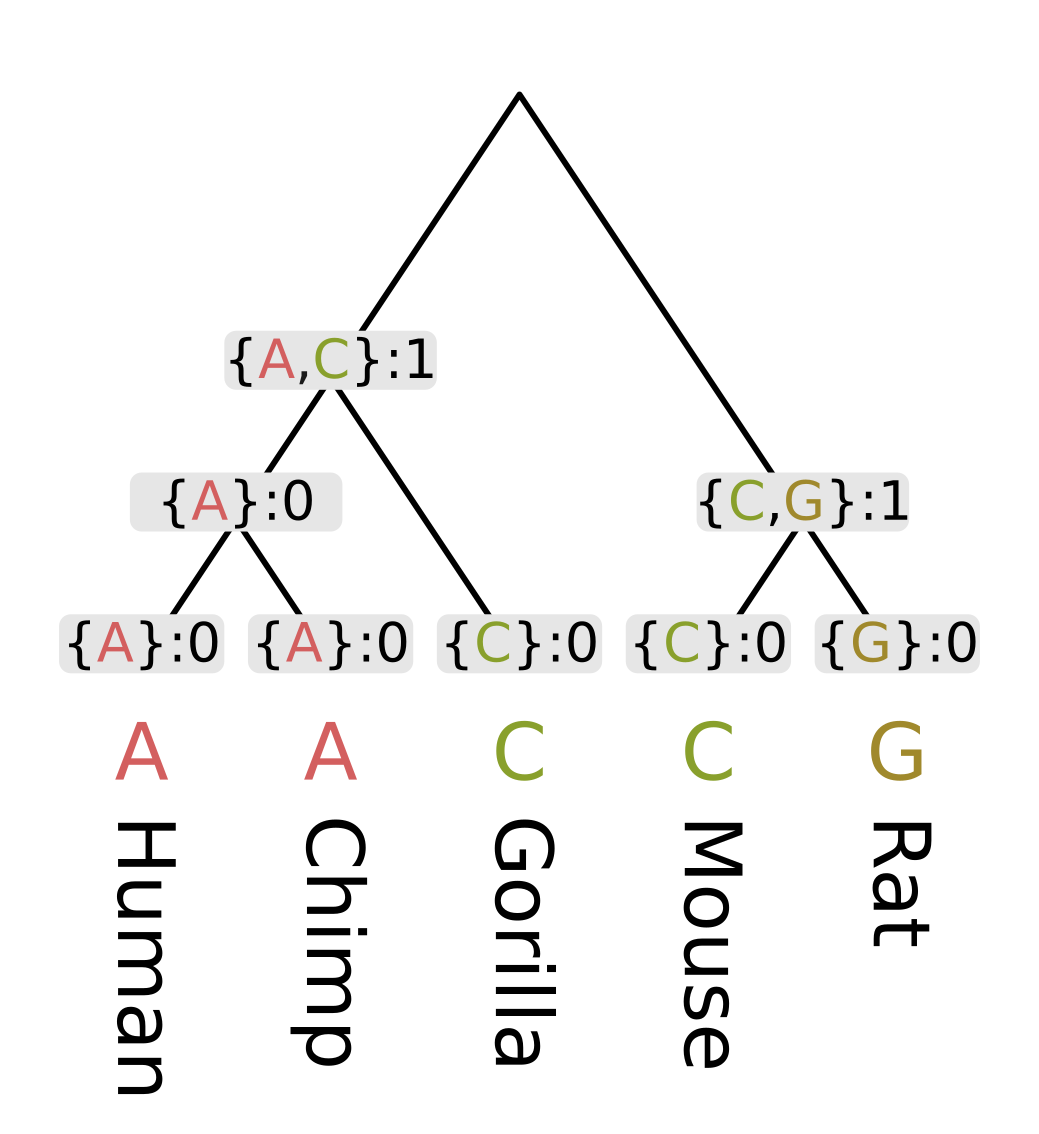
As an example, let’s consider a genomic position homologous between apes and rodents. At this position the nucleotide observed for humans and chimps is adenine (A), for gorillas and mice it is cytosine (C), and for rats it is guanine (G). We will compute the parsimony score for a given tree topology, in this case one what treats humans and chimps and sisters, and also mice and rats as sisters.

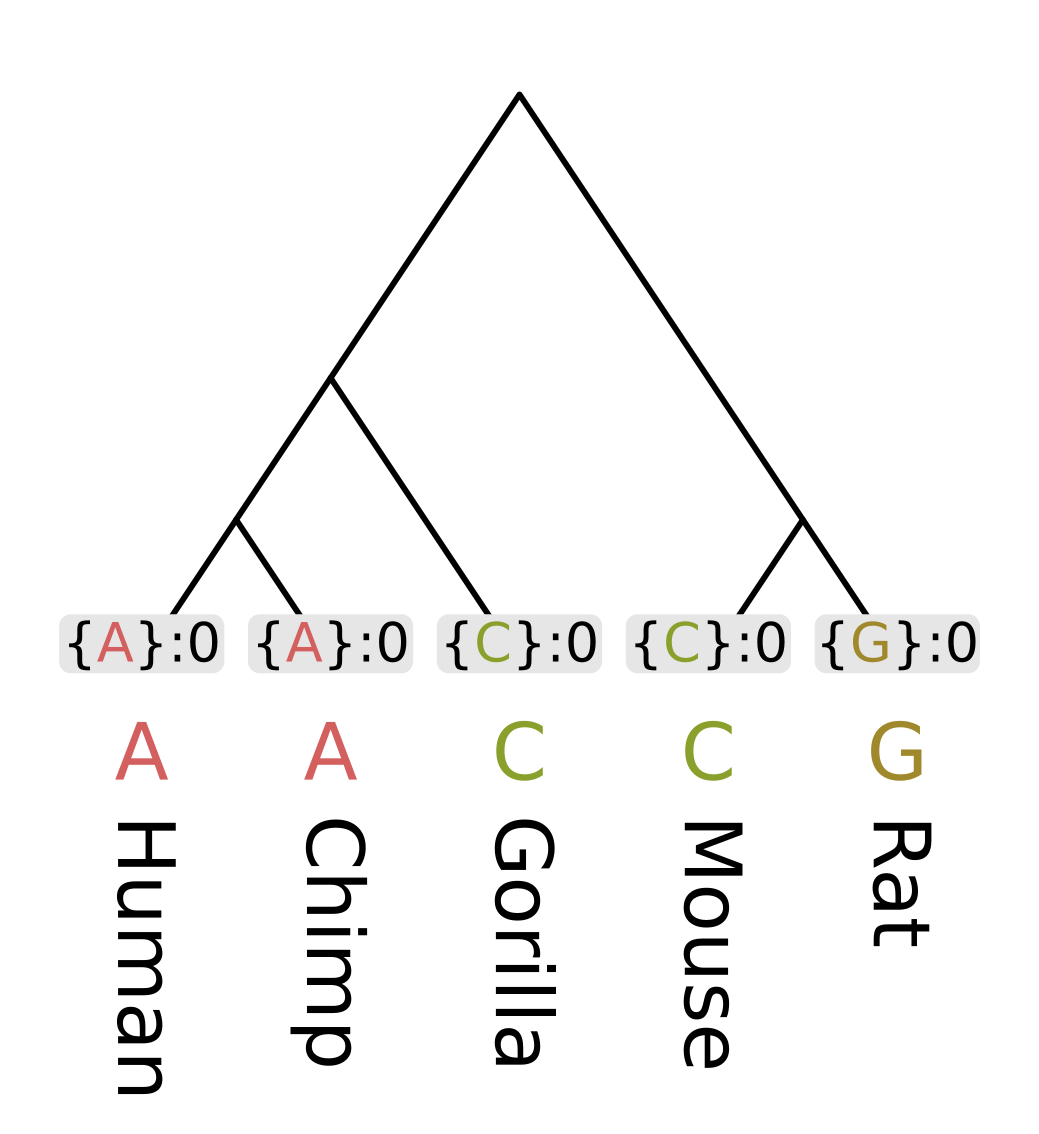
Like other dynamic programming algorithms for phylogenetic inference, we need initialize the values at each tip. For the Fitch algorithm, there are two different kinds of values at each node;

1. a set of most parsimonious states given the site pattern and topology under that node
2. the minimum number of changes required to explain the site pattern under given the topology under that node

For the tip nodes, each set has a single element corresponding to the observed state, and the minimum number of changes is always zero.

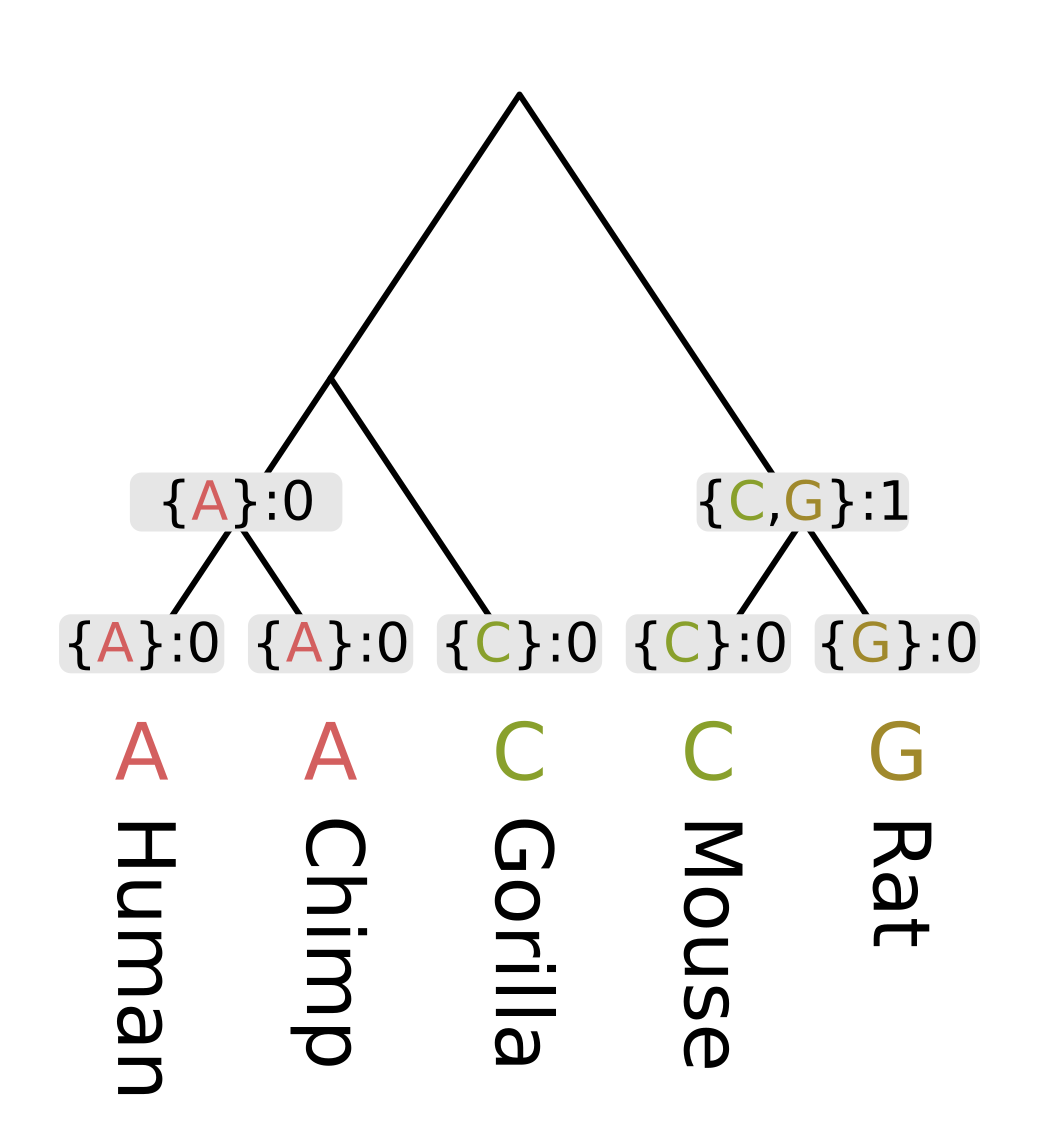
Then we need to recurse through the internal nodes of the tree, always visiting children before parents. The most straightforward way to accomplish this is postorder traversal. However, for this example we will use levelorder traversal, visiting the lowest level of nodes first, then the next lowest, until we get to the root.

For each node we first calculate the intersection of the sets of most parsimonious states from the node’s children. For humans and chimps the intersection contains a single state “A”, but for rodents the intersection is empty.

When the intersection is non-empty, we add all elements of the intersection to the set of most parsimonious states for a given node. A non-empty intersection also means that no changes are required along either branch leading to the children, as at least one most parsimonious state is present in all three sets (parent and two children).

Since no changes are required, we calculate the parsimony score for that node (the minimum number of required changes) by simply adding the parsimony score for the two children. In the case of humans and chimps, the intersection is {“A”} and the sum of parsimony scores is 0.

When the intersection is empty, we add all elements of the union to the set of most parsimonious states. For each state in the union, it will either be present in the parent and left child sets, or the parent and right child sets. In both cases we need at least one mutation to explain the pattern, but the mutation will be on the left or right branch respectively. So the parsimony score will be the sum of scores of the children, plus one. In the case of rodents, the union is {C, G} and the parsimony score will be 0 + 0 + 1 = 1.

For the ancestor of humans, chimps and gorillas (Homininae), the intersection of the human and chimp set on the left {A} and the gorilla set {C} is empty, so we use the union {A, C}. Since the intersection was empty, the parsimony score will be the sum of child scores plus one.

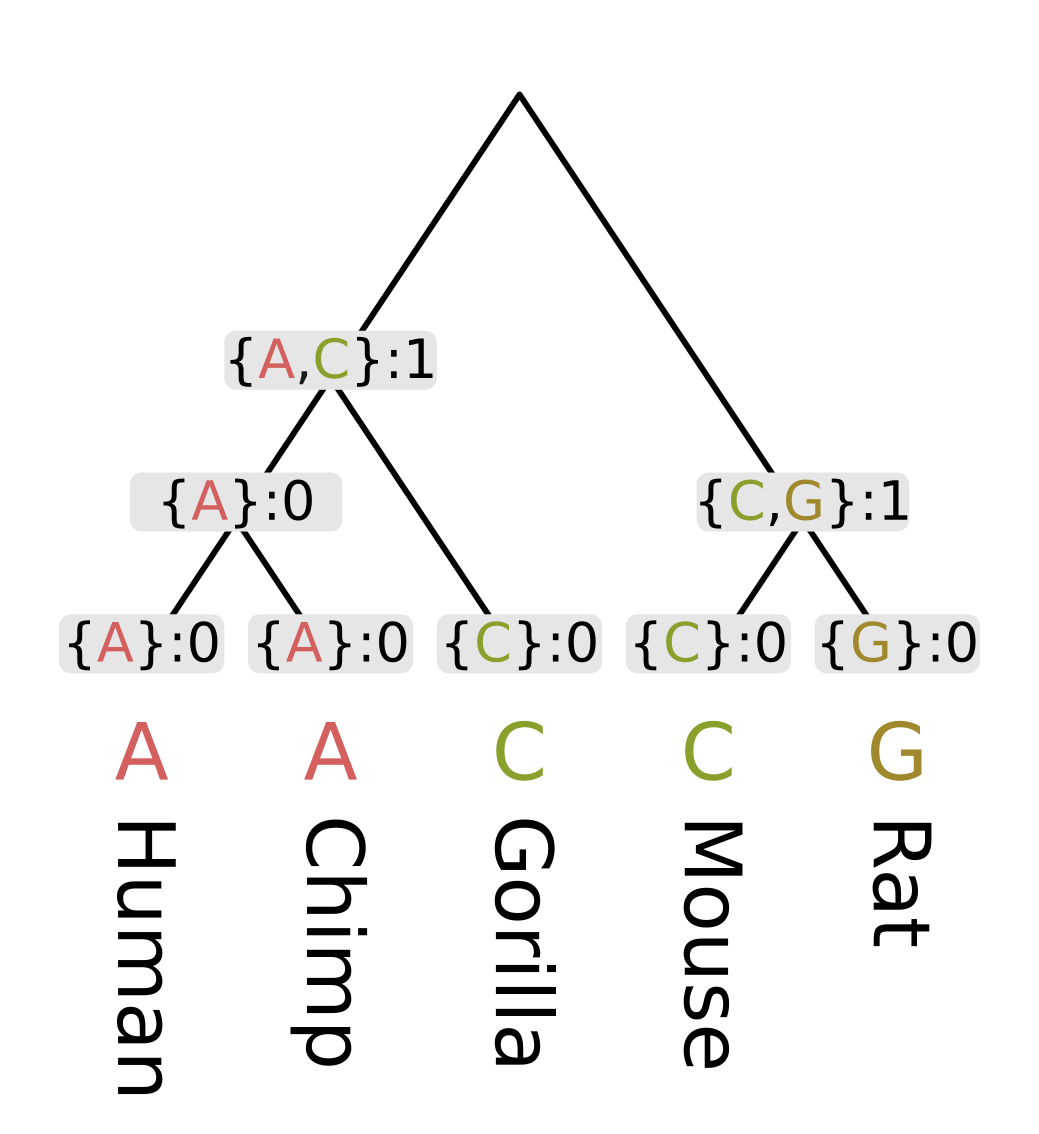
Finally at the root, the intersection of the ape set {A, C} and the rodent set {C, G} is nonempty, as C is present in both. So the most parsimonious state at the root will be C, and since this state is present in all three sets, we do not need to invoke changes and only need to sum the child scores. For this example this sum is 1 + 1 = 2.

Equal cost parsimony will derive the same score for any rooted tree with the same unrooted topology. In other words, neither the rooting nor the branch lengths affect the score in any way (at least in terms of inference). Given five taxa as in the above example, there are fifteen possible unrooted topologies:

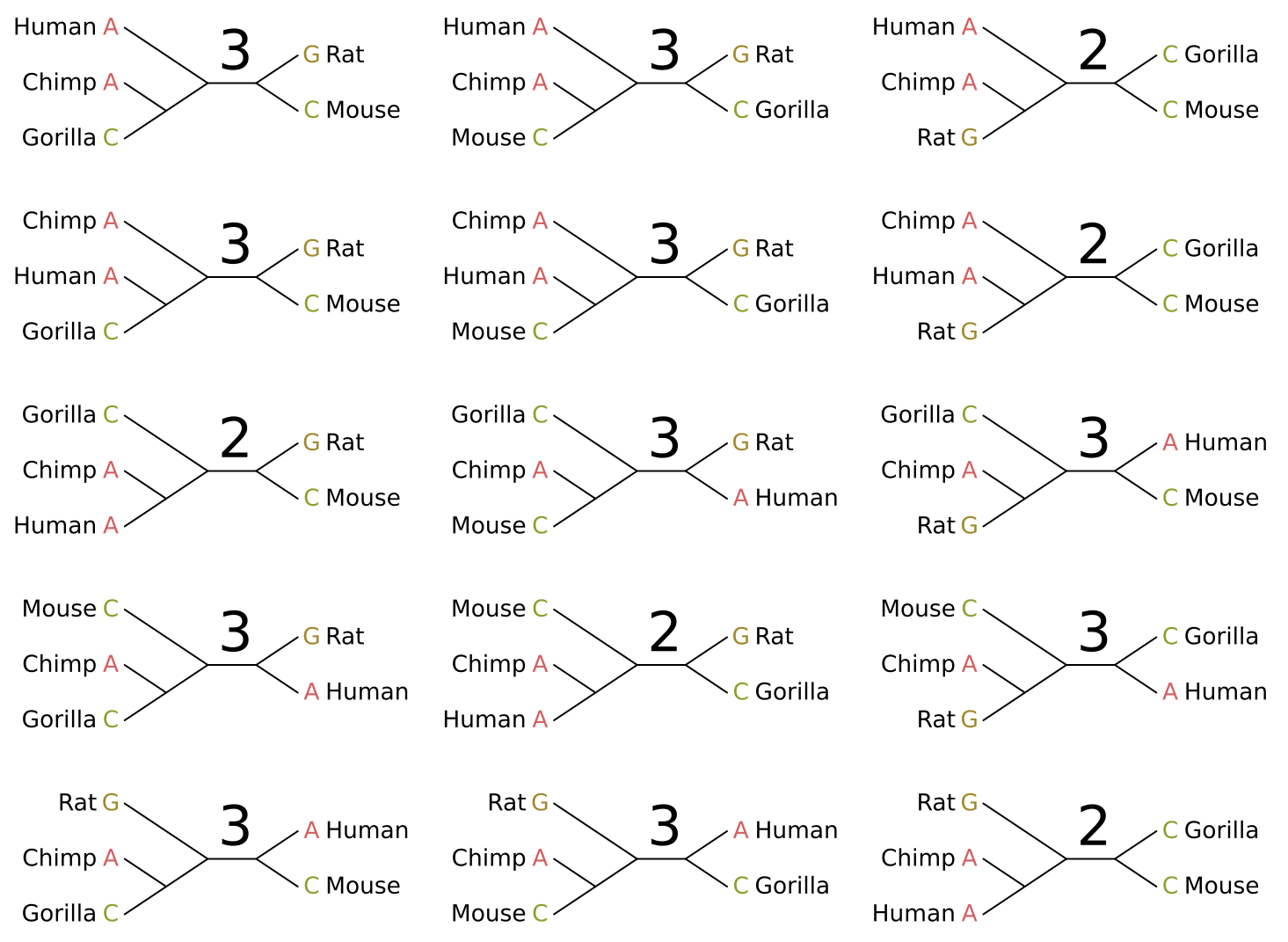
I have given the parsimony score for each topology given the site pattern. In this case there are five maximum parsimony solutions, and we cannot distinguish between them. Luckily one of these is the “true in real life” tree topology for these organisms (left middle).

The parsimony score of a multiple sequence alignment, or the character matrix of a set of traits, is the sum of parsimony scores for all sites in the alignment or all traits. By sampling enough sites and/or traits we should be able to identify a single optimal tree from its parsimony score.