Dollo’s law and unequal-cost parsimony
Certain mutations are more surprising than others. DNA is composed of a string of nucleotides, which are either pyrimadines (cytosine or thymine) or purines (adenine or guanine). A single point mutation to DNA is either a transition from one pyrimadine to another or one purine to another, or a transversion from a purine to a pyrimadine or vice versa. Transitions are biochemically easier than transversions, and hence much more commonly occuring in the evolution of genomes.
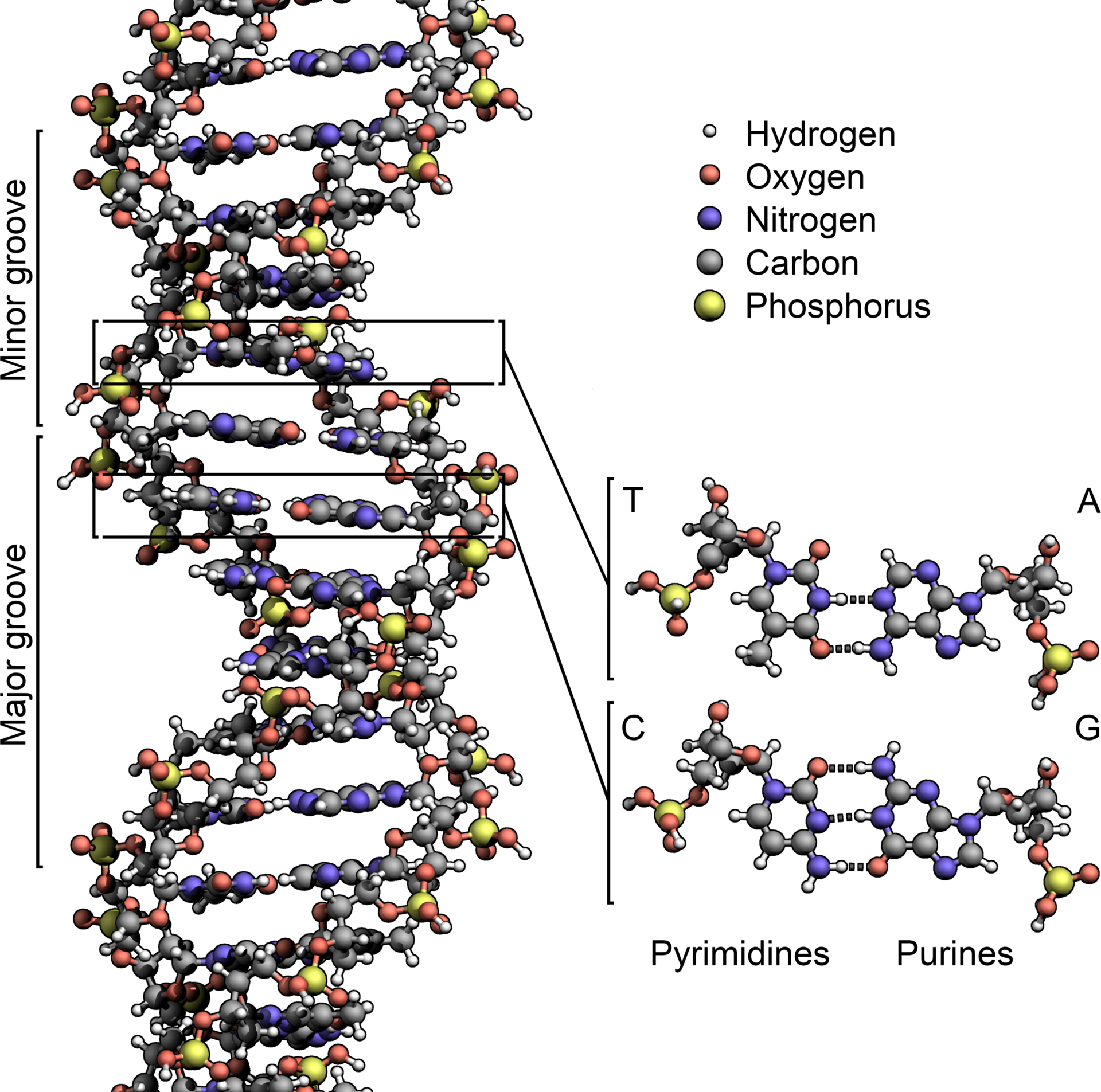
Image from Wikipedia user Zephyris
This principle also applies to traits. Dollo’s law states that complex characters, once lost from a lineage, are unlikely to be regained (Wright et al. 2015, Dollo 1893). For example, the evolution of flight in bats required the evolution of multiple components like wing membranes, a novel complex of muscles and low-mass bones (Cooper et al. 2010). Once any one of those components are lost the others are likely to be lost too. Because regaining the trait will require so many components to be regained, it is unlikely. Therefore we should be more surprised by a transition from flightlessness to flightedness than the reverse.
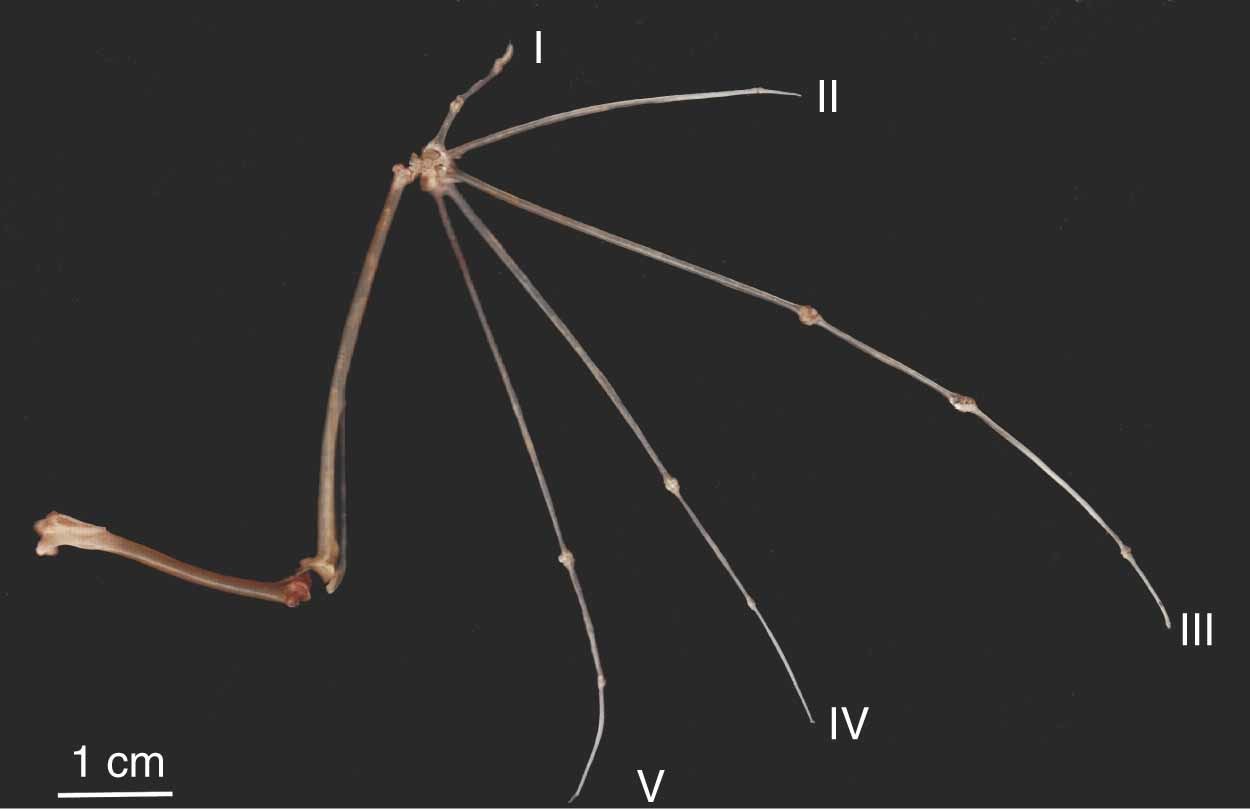
Figure 1 from Cooper et al. (2010) showing the thin elongated metacarpals and phalanges of Seba’s short‐tailed bat.
Equal-cost parsimony, for example when using the Fitch algorithm, does not account for this kind of difference in expectations. However unequal-cost parsimony uses a cost matrix to assign different costs to different transitions. For the DNA evolution example, it might look something like this:
| A | C | G | T | |
|---|---|---|---|---|
| A | 0 | 5 | 1 | 5 |
| C | 5 | 0 | 5 | 1 |
| G | 1 | 5 | 0 | 5 |
| T | 5 | 1 | 5 | 0 |
This cost matrix penalizes a transversion five times more than it penalizes a transition. For the trait evolution example, it might look something like this:
| . | + | - |
|---|---|---|
| + | 0 | 1 |
| - | Infinity | 0 |
In the above matrix, plus is used to indicate the presence of a trait (e.g. flight) and a minus indicates the absence. This kind of matrix is known as a Dollo model, where only forward transitions (from + to -, i.e. losing the trait) are allowed, and reverse transitions are prohibited. Using this model implies that the trait must have been present in the most recent common ancestor (MRCA) of all species in the tree, so it will be inappropriate to use when the trait was absent from the MRCA.
The Sankoff algorithm uses dynamic programming to efficiently calculate the parsimony score for a given tree topology and cost matrix. Let’s use the DNA cost matrix above to demonstrate it.
A vector is associated with every node of the tree. The size of the vector is the size of the alphabet for a character, so 2 for a binary trait like flight, 4 for DNA or 20 for proteins. Each element of the vector corresponds to one of the possible states for that character. Each element of the vector stores the parsimony score for the tree topology under a node, given the state at that node corresponding to the element, and the known tip states.
To initialize the tip node vectors, set the cost for the elements corresponding to known tip states to zero. The other states are known to be not true, so they should never be considered. This could be achieved by setting their cost to infinity, represented here by dots.
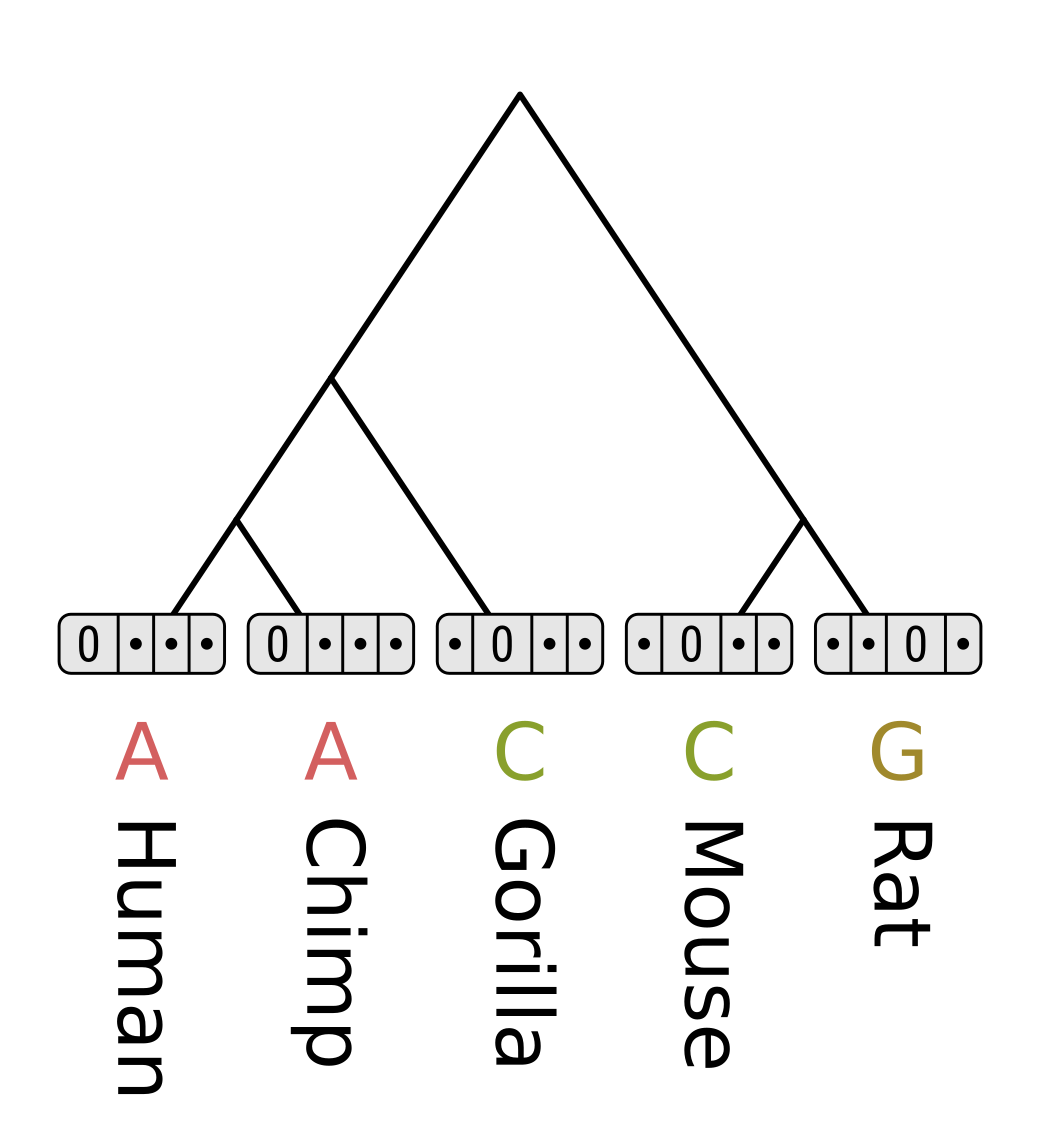
For each element of each internal node, we have to consider the cost of each possible transition for each child branch. The parsimony score for the element is the minimum possible cost for the left branch, plus the minimum possible cost for the right branch. The cost for each possible transition is the corresponding value from the cost matrix, plus the score in the corresponding child element.
Consider the MRCA of humans and chimps. For state A, the cost of transitioning to A in humans will be 0 + 0 = 0, to C will be 5 + ∞ = ∞, to G will be 1 + ∞ = ∞, and to T will be 5 + ∞ = ∞. The minimum for the left branch for the left branch is therefore 0. Since chimps have the same state as humans in this example, the cost will be the same, and the sum of minimum costs will be 0.
Repeat for C, G and T.
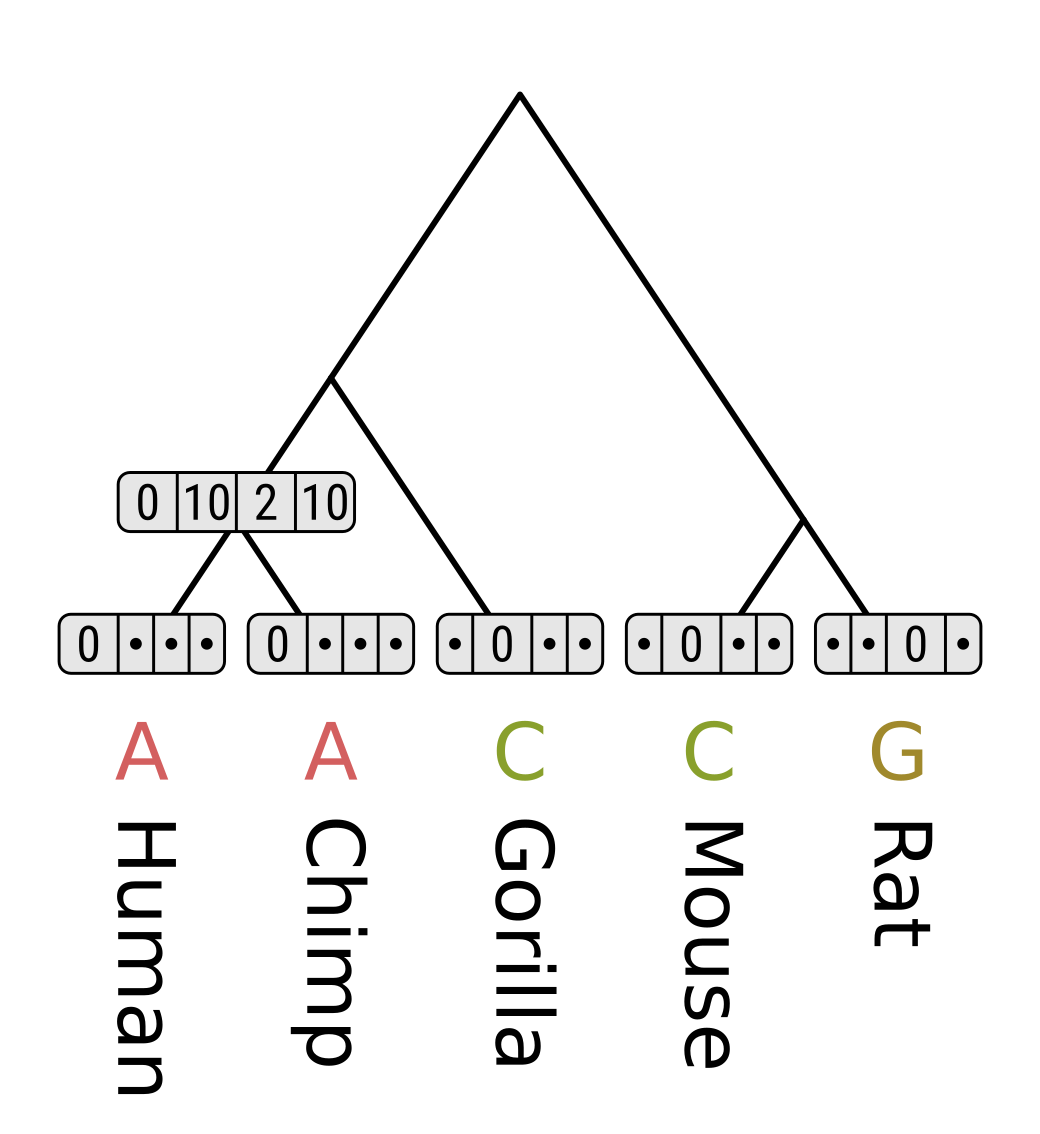
Now consider the MRCA of humans, chimps and gorillas. For state A, the cost of transitioning to A in the human/chimp MRCA will be 0 + 0 = 0, to C will be 5 + 10 = 15, to G will be 1 + 2 = 3, and to T will be 5 + 10 = 15. So the minimum along the left branch is 0. The cost of transitioning from A to C in gorillas will be 5 + 0 = 5, and from A to other gorilla states will be ∞. Therefore the minimum cost along the right branch is 5, and the parsimony score for state A is 0 + 5 = 5.
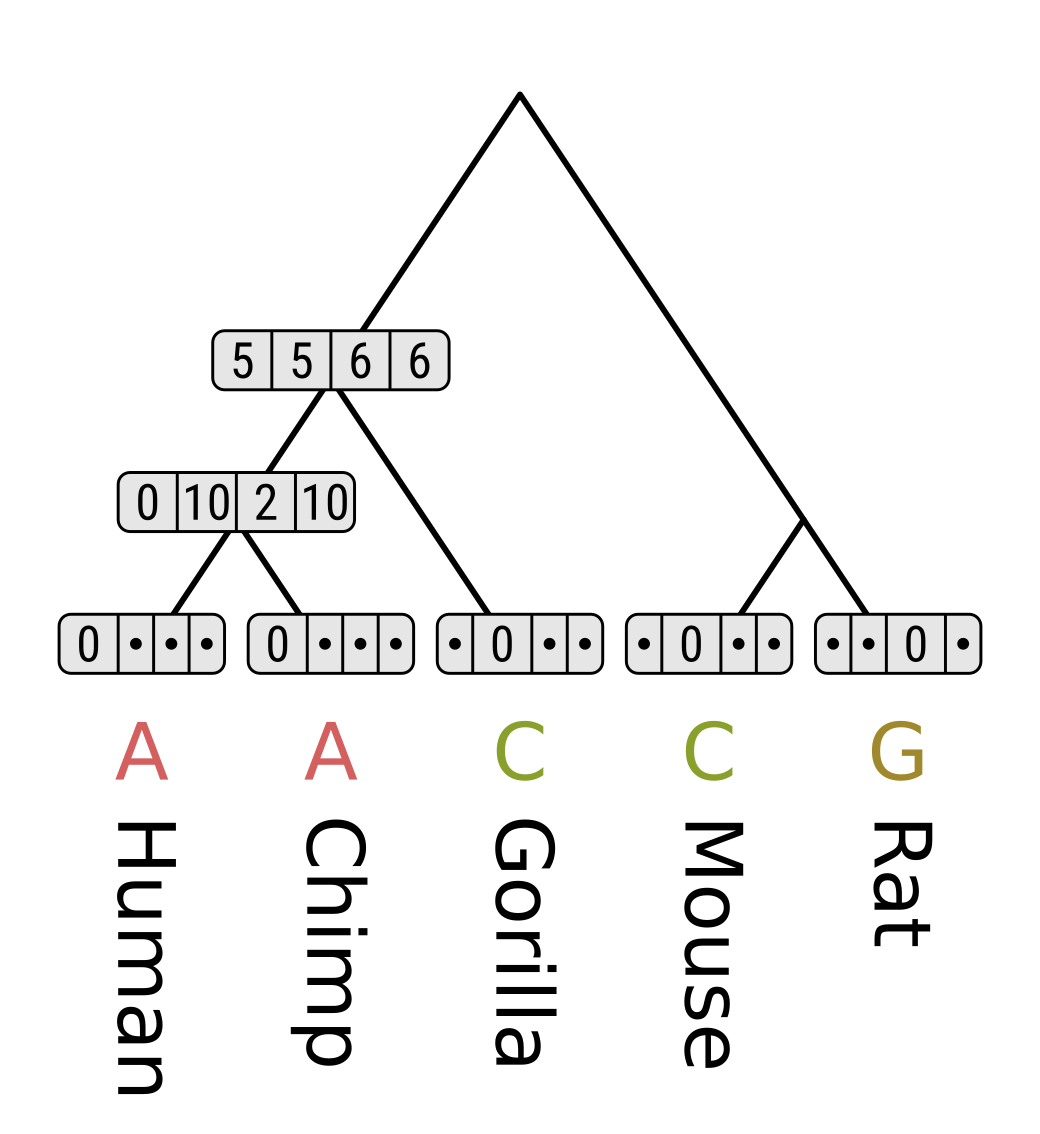
Repeat the above for the remaining nodes. Here we are walking the tree postorder, but like for the Fitch algorithm levelorder would work too.
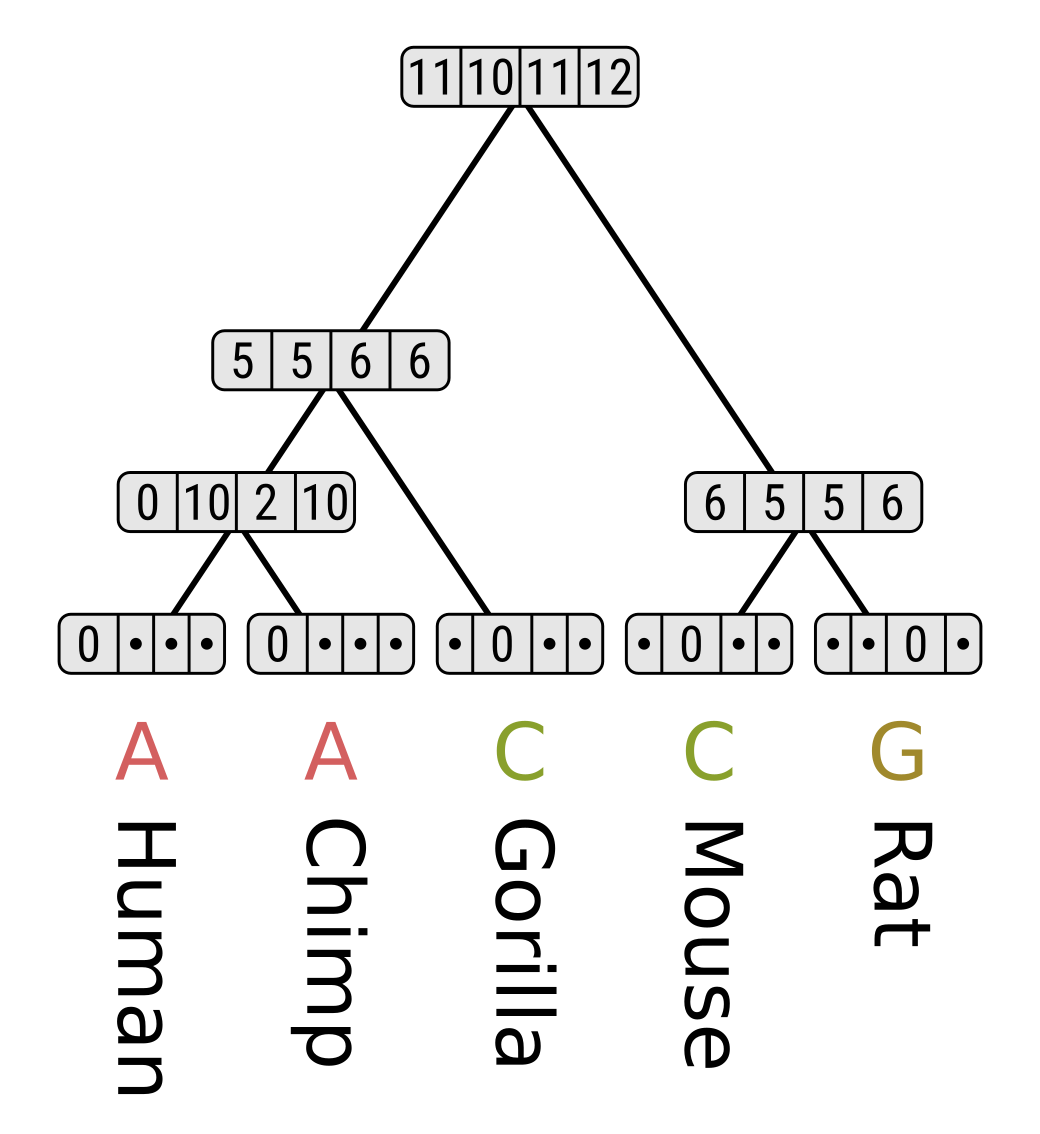
Finally, the parsimony score for the entire tree is the minimum score out of the root states - for this tree and site pattern, 10. As with equal-cost parsimony, the score for an entire multiple sequence alignment or character matrix is the sum of parsimony scores for each position or for each character respectively.
