Recursion

Recursion is where a single function inside a computer program calls itself. This turns out to be an extremely versatile tool in the computer science toolbox. Consider the following toy example where we can use recursion to solve factorials.

The solution to n! is n×n-1×n-2×n-3×…×1. For example the solution to 5! is 5×4×3×2 = 120. Notice that we can also arrive at this solution by multiplying 4! by 5, we can arrive at 4! by multiplying 3! by 4, and so on.

We can therefore write a recursive function that calls itself called factorial:

factorial(n):
	(n - 1)! = factorial(n - 1)
	n! = (n - 1)! × n

	return n!

What’s wrong with the above function? It will never stop calling itself! Consider if we made the function call factorial(5):

factorial(5):
	(5 - 1)! = factorial(4):
		(4 - 1)! = factorial(3):
			(3 - 1)! = factorial(2):
				(2 - 1!) = factorial(1):
					(1 - 1!) = factorial(0):
						(0 - 1!) = factorial(-1):
							...

To make it work, we can add a conditional if...else statement (also known as branching) inside the recursive function. We know that the value of 1! is 1, so when factorial(1) is called, let’s simply set n! to 1.

factorial(n):
	if n == 1:
		n! = 1
	else:
		(n - 1)! = factorial(n - 1)
		n! = (n - 1)! × n

	return n!

When the function is called, the recursion will now proceed downwards to factorial(1), then back upwards via the return statements. Again imagine we call factorial(5) (hereafter f(n)). This will create a cascade of recursion where the function calls where f(5) calls f(4), which calls f(3), which calls f(2), which finally calls f(1). Then, f(2) will return 1, f(2) will return 2, f(3) will return 6, f(4) returns 24, then finally f(5) returns the final value of 120:

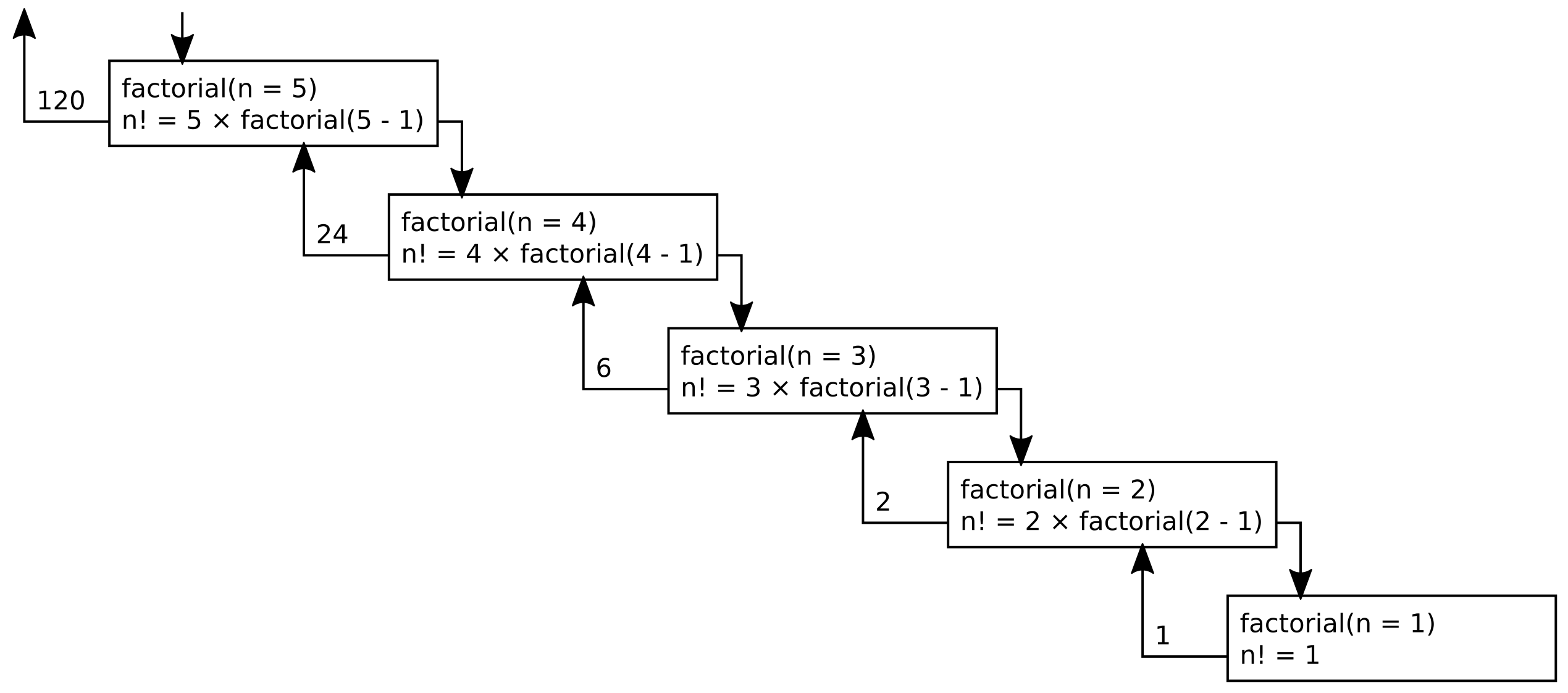
Now you know how to use recursion!